Question

In which of the following, the image of an object placed at infinity will be highly diminished and point sized?
A. Concave mirror only
B. Convex mirror only
C. Convex lens only
D. Concave mirror, convex mirror, concave lens and convex lens.

Answer 1

Hint:Ray diagrams assist us in tracing the path of light for a person viewing a point on an image of an item. The incident and reflected rays are represented by lines with arrows in a ray diagram. It also aids us in determining the direction of the light.

Complete step by step answer:
When light rays from infinity strike a concave mirror, convex mirror, concave lens, or convex lens, a drastically decreased picture is generated at the focus, as illustrated in the figure.
The mirror equation and lens equation can be used to confirm this.
Mirror Equation is given by: $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Lens Equation is given by: $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Substituting \[u = - \,\infty \] , \[v = f\]
Magnification \[m = \dfrac{v}{u} = \dfrac{f}{\infty } = 0\]
Hence, the image is point size.

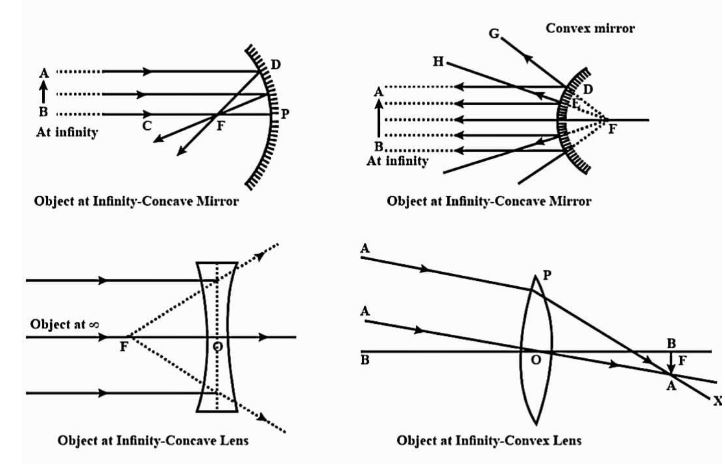
So, the correct option is D.

Note: The focal length of all optical lenses is the distance from the lens to the focus point along the optical axis of the lens. The focal length of a lens is determined by three factors: the radius of curvature of the lens, the refractive index of the substrate from which the lens is constructed, and the medium in which the lens sits. Lenses with a highly curved shape and a high refractive index that are placed in a medium with a big difference in refractive index will have a shorter focal length and thus be more powerful. A lens' focal length can be estimated using the lens manufacturer's formula.