Question

In $\vartriangle ABC$, $P,Q,R$ are the midpoints of sides $AB,BC,AC$ respectively. If the area of $ABC$ is $120c{m^2}$, find areas of $PQR,PQCR,PBRCQ$.

Answer 1

Hint:Since $P,Q,R$ are the midpoints of $\vartriangle ABC$, we can use the Midpoint theorem of triangles to solve this question. Thus we get the relation between $PR$ and $BC$. Also using the congruence relations of the triangles, we can find the required areas.

Formula used:In $\vartriangle ABC$, if $P,Q,R$ are the midpoints of the sides
$AB,BC,AC$ respectively, then according to the midpoint theorem of triangles we have,
$ \Rightarrow PR\parallel BC$ and $PR = \dfrac{1}{2}BC$.
Also, the four triangles $\vartriangle APR,\vartriangle ABQ,\vartriangle PQR,\vartriangle RQC$ are congruent.

Complete step-by-step answer:
Given that $P,Q,R$ are the midpoints of sides $AB,BC,AC$ of $\vartriangle ABC$ respectively and $Area\vartriangle ABC = 120c{m^2}$
We need to find the areas of $PQR,PQCR,PBCQ$.

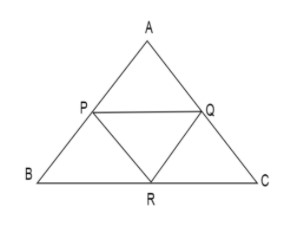
By midpoint theorem we have,
In $\vartriangle ABC$, if $P,Q,R$ are the midpoints of the sides $AB,BC,AC$ respectively, then
$ \Rightarrow PR\parallel BC$ and $PR = \dfrac{1}{2}BC$.
Also, the four triangles $\vartriangle APR,\vartriangle ABQ,\vartriangle PQR,\vartriangle RQC$ are congruent.
Congruence of triangles implies equal sides and equal angles.
Therefore the area is the same for congruent triangles.
$ \Rightarrow Area\vartriangle APR = Area\vartriangle PBQ = Area\vartriangle PQR = Area\vartriangle RQC$
Also since all these four triangles together constitute the larger triangle $\vartriangle ABC$, we have each of these smaller triangles have an area equal to one fourth of the area of $\vartriangle ABC$.
Given, Area of $\vartriangle ABC = 120c{m^2}$
This implies each of the four smaller triangles have area $\dfrac{1}{4} \times Area\vartriangle ABC = \dfrac{1}{4} \times 120 = 30c{m^2}$.
$ \Rightarrow Area\vartriangle PQR = 30c{m^2}$
Also, $PQCR$ contains two congruent triangles $\vartriangle PQR,\vartriangle RQC$ both with area $30c{m^2}$.
$ \Rightarrow AreaPQCR = 30c{m^2} + 30c{m^2} = 60c{m^2}$
In the same way, $PBCQ$ contains three congruent triangles $\vartriangle PBR,\vartriangle PQR,\vartriangle RQC$ all with area $30c{m^2}$.
$ \Rightarrow Area PBCR = 3 \times 30c{m^2} = 90c{m^2}$

Note:Midpoint theorem is applicable only when a triangle is formed by joining midpoints of three sides. If the triangle formed has two vertices on midpoints of two sides and the third vertex is any point on the third side, this result is not applicable.