Question

In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.

Answer 1

Hint: First of all, draw the diagram for the given problem by using suitable construction along with the given data. As we can draw an infinite number of chords, here we consider any two chords to prove that all the chords are of equal. So, use this concept to reach the solution of the given problem.

Complete step by step solution:
Construction: Let the two concentric circles are \[{C_1}\] and \[{C_2}\] with centre \[O\]. \[AB\] and \[CD\]are the chords of the outer circle \[{C_1}\], such that they touch the inner circle \[{C_2}\] at \[E\] and \[F\] respectively. Join \[OA,OB,OC,OD,OE\& OF\].

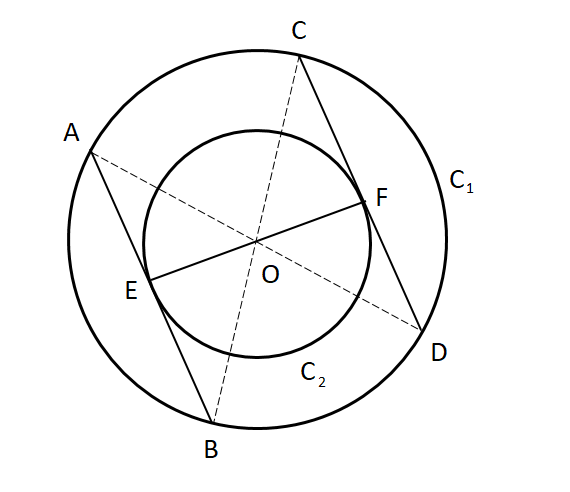
Now, we have to prove that the chords of the outer circle which touch the inner circle are of equal length i.e., \[AB = CD\].
We know that tangent at any point of the circle is perpendicular to the radius through the point of contact.
As, \[OE \bot AB\] we have \[\angle OEA = {90^0}\]
Similarly, \[\angle OFC = {90^0}\]
Therefore, \[\angle OEA = \angle OFC = {90^0}...........................................................\left( 1 \right)\]
Now, in right \[\Delta AQE\] and \[\Delta COF\]
\[
   \Rightarrow OA = OC{\text{ }}\left[ {{\text{radii of the circle}}} \right] \\
   \Rightarrow OE = OF{\text{ }}\left[ {{\text{radii of the circle}}} \right] \\
   \Rightarrow \angle OEA = \angle OFC = {90^0}{\text{ }}\left[ {{\text{from equation }}\left( 1 \right)} \right] \\
\]
Thus, by R.H.S congruence rule \[\Delta AOE \cong \Delta COF\].
So, \[EA = FC.....................................\left( 2 \right)\]
Similarly, \[EB = FD....................................\left( 3 \right)\]
Adding equation \[\left( 2 \right)\] and equation \[\left( 3 \right)\], we get
\[
   \Rightarrow EA + EB = FC + FD \\
  \therefore AB = CD \\
\]
Hence proved that all chords of the outer circle which touches the inner circle are of equal length.

Note: In two right angles triangles, if the length of the hypotenuse and one side of the triangle, is equal to the length of the hypotenuse and the corresponding side of the other triangle, then the two triangles are congruent by R.H.S congruence rule.