Question

In triangle ABC, P is the midpoint of side BC. A line through p and parallel to CA meets AB at point Q; and a line through Q meets at S. QS parallel to BC meets median AP at point R. Prove that:
(I) AP = 2AR
(II) BC = 4QR

Answer 1

Hint: For solving this problem, the knowledge of the midpoint theorem in a triangle is necessary. By drawing the figure, we can easily apply the midpoint theorem in suitable triangles to obtain the desired result.
Complete step-by-step answer:

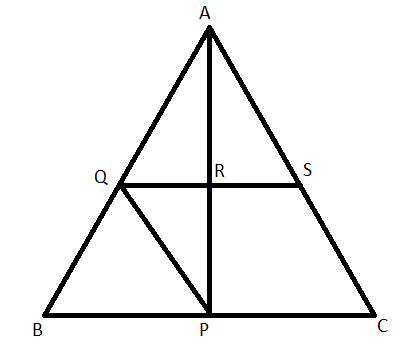
Given: In triangle ABC, P is the midpoint of BC. Also, PQ is parallel to CA and meets AB at point Q. QS is parallel to BC and meets AP at point R.
To prove: AP = 2AR and BC = 4QR.
Proof:
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
In triangle ABC, P is the midpoint of BC and PQ is parallel to AB. Now, by using the converse of the midpoint theorem, Q is the midpoint of AB.
In triangle ABP, Q is the midpoint of AB and QR is parallel to BP. Again, by using the converse of the midpoint theorem, R is the midpoint of AP.
So, we concluded that AP = 2AR.
For, proving the part (ii), consider triangle ABP which is having Q as the midpoint of AB and R as the midpoint of AP. Now, by using the midpoint theorem:
$QR=\dfrac{1}{2}BP$
Replacing BP as half of BC as P is the midpoint of BC, we get
$\begin{align}
  & QR=\dfrac{1}{2}\left( \dfrac{1}{2}BC \right) \\
 & QR=\dfrac{1}{4}BC \\
 & \therefore BC=4QR \\
\end{align}$
So, we proved both the parts individually.
Note: The key concept involved in solving the problem is the knowledge of midpoint theorem. By using the result obtained as a consequence of the midpoint theorem, we easily proved required statements. This knowledge is very helpful in solving complex problems.