Question

In triangle ABC, $\overline{AB}=\overline{AC}$ and $\angle A=40{}^\circ $ . Point O is within the triangle with $\angle OBC=\angle OCA$ . Find the measure of $\angle BOC$ .
(A). $110{}^\circ $
(B). $35{}^\circ $
(C). $140{}^\circ $
(D). $70{}^\circ $

Answer 1

Hint: Start by using the property that angles opposite to equal sides are equal followed by the theorem that the sum of all the angles of a triangle is equal to $180{}^\circ $ .

Complete step-by-step solution -
Let us start the above question by drawing the diagram of the situation given in the question.
 

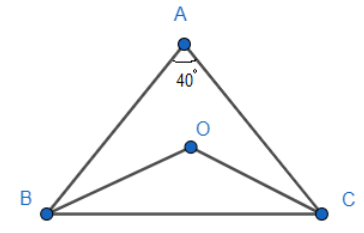
Now applying the property that angles opposite to equal sides of a triangle are equal in $\Delta ABC$, in which it is given that AB=AC, we get
 $\angle ABC=\angle ACB................(i)$
Now using the figure, we can write our expression as:
$\angle OBC+\angle OBA=\angle OCB+\angle OCA$
It is given in the question that $\angle OBC=\angle OCA$ . Using this, we get
$\angle OBA=\angle OCB.............(ii)$
We also know that the sum of all the angles of a triangle is equal to $180{}^\circ $ .
$\therefore \angle ABC+\angle ACB+\angle CAB=180{}^\circ $
Now we will put the known value of $\angle A$ in the equation. On doing so, we get
$\therefore \angle ABC+\angle ACB+\angle CAB=180{}^\circ $
$\Rightarrow \angle ABC+\angle ACB+40{}^\circ =180{}^\circ $
$\Rightarrow \angle ABC+\angle ACB=140{}^\circ $
Now using equation (i), we can write the equation as:
$2\angle ABC=2\angle ACB=140{}^\circ $
$\Rightarrow \angle ABC=\angle ACB=70{}^\circ $
Now applying the angle sum property of a triangle for triangle OBC, we get
$\angle OBC+\angle OCB+\angle BOC=180{}^\circ $
Now if we substitute the value of $\angle OCB$ from equation (ii), we get
 $\angle OBC+\angle OBA+\angle BOC=180{}^\circ $
$\Rightarrow \angle ABC+\angle BOC=180{}^\circ $
Now according to the results we found above, $\Rightarrow \angle ABC=\angle ACB=70{}^\circ $ .
$\therefore 70{}^\circ +\angle BOC=180{}^\circ $
$\Rightarrow \angle BOC=110{}^\circ $
Therefore, the measure of angle BOC is $110{}^\circ $ . Hence, the correct answer is option (a).

Note: It is prescribed to learn all the basic theorems related to triangles as they are regularly used in the questions. It is also prescribed that you always start a geometry related problem by drawing the diagram, as it may give you a better visualisation of the situation given in the question.