Question

In triangle ABC, D is a point in side AB such that AB=4AD and E is a point in C such that AC= 4AE. Then BC: DE= 4:3. If the above statement is true then mention the answer as 1, else mention 0 if false.

Answer 1

Hint: In order to solve this question we need to prove that $\Delta $ ADE and $\Delta $ ABC are similar , we will do it with the help of basic proportionality theorem which states that “ If a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio”.

Complete step-by-step answer:

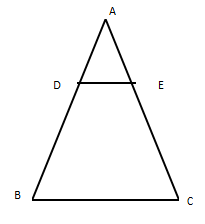
Given statement is “D and E are the points on side AB and BC of $\Delta $ ABC respectively”. Join DE

Given that AB = 4AD and AC = 4AE

We need to prove that the $\Delta $ ADE and $\Delta $ ABC are similar. Where, A is the common angle in $\Delta $ ADE and $\Delta $ ABC.

Therefore, \[\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}{\text{ }}\left[ {By{\text{ basic proportionality theorem}}} \right]\]

Then, $\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{ED}}{{BC}}................(1)$
So, $\Delta ABC \cong \Delta ADE{\text{ }}\left[ {{\text{By SAS criteria}}} \right]$
${\text{As, }}\dfrac{{AD}}{{AB}} = \dfrac{1}{4}.............(2)$
And $\dfrac{{AE}}{{AC}} = \dfrac{1}{4}...............(3)$
On comparing (1), (2) and (3), we get
$\dfrac{{ED}}{{BC}} = \dfrac{1}{4}{\text{ or }}\dfrac{{DE}}{{BC}} = \dfrac{1}{4}$

Hence, \[BC = 4DE{\text{ or }}\dfrac{{BC}}{{DE}} = \dfrac{1}{4}\]
So, the given statement is false. Answer is 0.

Note: The above problem is based on the use of basic theorems of triangles. To solve these types of problems learn all the theorems related to triangles and the basic criteria to prove the similarity of triangles whether it is SAS, AAS, AAA, SSS. In this problem we use the proportionality theorem of triangle and other such theorems are Exterior angle theorem, Pythagoras theorem and many more.