Question

In triangle ABC, ∠A = 90°, AD is perpendicular to BC and AD = BD = 2cm. The length of CD is
$
  {\text{A}}{\text{. 3cm}} \\
  {\text{B}}{\text{. 3}}{\text{.5cm}} \\
  {\text{C}}{\text{. 3}}{\text{.2cm}} \\
  {\text{D}}{\text{. 2cm}} \\
$

Answer 1

Hint: To find the length of CD, we use the formula, square of perpendicular = product of segments, in a right angled triangle.

Complete step-by-step answer:

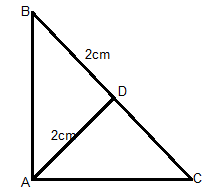
Given Data, ∠A = 90°, hence it is a right angles triangle.
Hence the line coming from angle ∠A perpendicular to its hypotenuse BC divides BC equally. I.e. BD = DC.
Therefore CD = 2cm.

To verify this we use the formula, Square of perpendicular = Product of segments

AD = perpendicular and BD, CD are the segments

$
   \Rightarrow {\text{A}}{{\text{D}}^2} = {\text{BD}} \times {\text{CD}} \\
   \Rightarrow {2^2} = 2 \times {\text{CD}} \\
   \Rightarrow {\text{CD = }}\dfrac{4}{2} = 2{\text{cm}} \\
$
Hence, CD = 2cm.
Therefore Option D is the correct answer.

Note: The key in solving such types of problems is to know the concept of a right angles triangle and the relation between the angle and the hypotenuse. Also, the concept of the square of the perpendicular is equal to the product of segments is to be known.