Question

In three line segments OA, OB, and OC points L, M, N respectively are chosen so that LM is parallel to AB and MN is parallel to BC but neither of L, M, N nor of A, B, C is collinear. Show that LN is parallel to AC.

Answer 1

Hint: According to the proportionality theorem that if a line is drawn parallel to one side of a triangle intersecting the remaining two sides at distinct points, then the remaining two sides get divided in the same ratio. In \[\Delta OAB\] , we have LM as parallel to AB. Now, using the proportionality theorem, we have, \[\dfrac{OL}{LA}=\dfrac{OM}{MB}\Rightarrow \dfrac{LA}{OL}=\dfrac{MB}{OM}\] . Now, add 1 to LHS and RHS of the equation \[\dfrac{LA}{OL}=\dfrac{MB}{OM}\] . Similarly, in \[\Delta OBC\] , we have, MN is parallel to BC (given). Now, using the proportionality theorem, we have, \[\dfrac{OC}{ON}=\dfrac{OB}{OM}\] . Solve it further and use the converse of proportionality theorem to get the required answer.

Complete step-by-step answer:
According to the question, it is given that in three-line segments OA, OB, and OC points L, M, N respectively are chosen so that LM is parallel to AB and MN is parallel to BC but neither of L, M, N nor of A, B, C is collinear.
We know the proportionality theorem that if a line is drawn parallel to one side of a triangle intersecting the remaining two sides at distinct points, then the remaining two sides get divided in the same ratio ………………………………………(1)

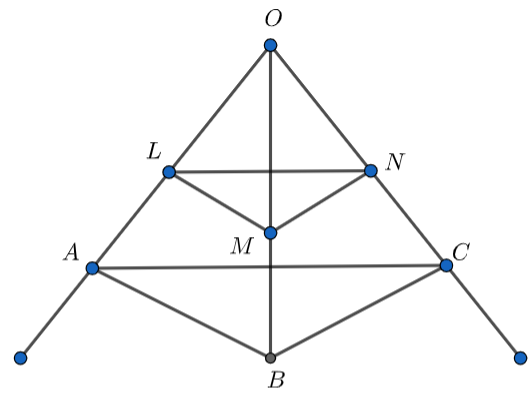
In \[\Delta OAB\] , we have
LM is parallel to AB (given)
Now, using the theorem shown in equation (1), we have
\[\Rightarrow \dfrac{OL}{LA}=\dfrac{OM}{MB}\]
\[\Rightarrow \dfrac{LA}{OL}=\dfrac{MB}{OM}\] ……………………………………….(2)
Now, on adding 1 in LHS and RHS of equation (2), we get
\[\Rightarrow \dfrac{LA}{OL}+1=\dfrac{MB}{OM}+1\]
\[\Rightarrow \dfrac{LA+OL}{OL}=\dfrac{MB+OM}{OM}\] …………………………………….(3)
From the figure, we can say that
\[LA+OL=OA\] ……………………………………(4)
\[OM+MB=OB\] ………………………………………(5)
From equation (3), equation (4), and equation (5), we get
\[\Rightarrow \dfrac{OA}{OL}=\dfrac{OB}{OM}\] ………………………………………….(6)
Similarly, in \[\Delta OBC\] , we have
MN is parallel to BC (given).
Now, using the theorem shown in equation (1), we have
\[\Rightarrow \dfrac{OC}{ON}=\dfrac{OB}{OM}\] ………………………………………….(7)
Now, from equation (6) and equation (7), we get
\[\Rightarrow \dfrac{OA}{OL}=\dfrac{OC}{ON}\] ………………………………………..(8)
In \[\Delta OAC\] , we have
\[\Rightarrow \dfrac{OA}{OL}=\dfrac{OC}{ON}\]
Since \[\dfrac{OA}{OL}=\dfrac{OC}{ON}\] , so using the converse of the property shown in equation (1), we can say that the line LN is parallel to AC.
Therefore, LN is parallel to AC.
Proved.

Note: Whenever this type of question is asked where there are line segments and we are asked to prove two lines parallel. For this type of questions, always try to use the proportionality theorem. Using the proportionality theorem will make the approach simpler and we will easily get the required result.