Question

In this given figure, ABCD and BPQ line. BP = BC and DQ || CP. Prove that
(I) CP = CD
(II) DP bisects angle CDQ.

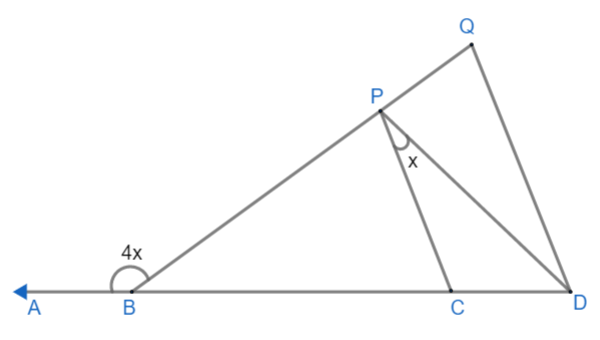
Answer 1

Hint: In this question, we are given BP = BC and DQ || CP. Also, $\angle ABP=4x\text{ and }\angle CPD=x$ We need to prove that CP = CD and DP bisects $\angle CDQ$ which means $\angle CDP=\angle PDQ$. For this, we will use the following properties of the triangle, lines, and angles:
(I) Exterior angle product: Exterior angle of a triangle is equal to the sum of the interior opposite angles.
(II) Isosceles triangle property: Angles corresponding to equal sides is an isosceles triangle and are always equal.
(III) Converse of isosceles triangle property: If two angles are equal in a triangle, then the corresponding side of equal angles are also equal.
(IV) If two lines are parallel and a transversal forms corresponding angles with parallel lines then corresponding angles are equal.

Complete step-by-step solution
Here we are given the diagram as:

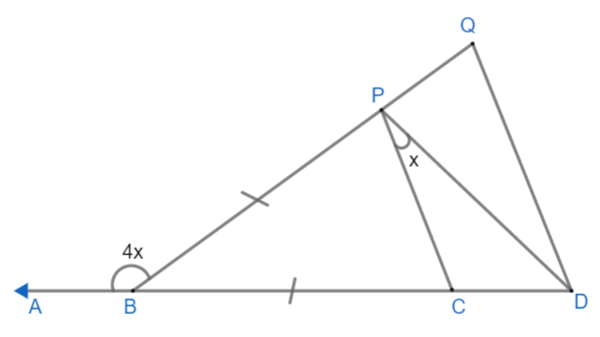
Here BP = BC, \[DQ\parallel CP,\angle ABP=4x\text{ and }\angle CPD=x\].
(i) Firstly, we need to prove CP = CD.
As we can see from triangle BPC that BP = BC, therefore $\angle BPC=\angle BCP$ because of isosceles triangle property, according to which angles corresponding to equal sides are also equal. Hence,
$\angle BPC=\angle BCP\cdots \cdots \cdots \left( 1 \right)$.
Now as we can see $\angle ABP$ acts as an exterior angle to $\Delta BPC$.
So using exterior angle property, which states that, an exterior angle is equal to the sum of two opposite interior angles, we get:
$\angle ABP=\angle BPC+\angle BCP$.
From (1), $\angle BPC=\angle BCP$.
Also, $\angle ABP=4x$ so we get:
$4x=\angle BCP+\angle BCP\Rightarrow 4x= 2\angle BCP\Rightarrow 2x=\angle BCP$
Hence $\angle BCP=\angle BPC=2x$.
Now using exterior angle property in the $\Delta PCD$ where $\angle BCP$ is the exterior angle and $\angle CPD\text{ and }\angle CDP$ are opposite interior angles, we get $\angle BCP=\angle CPD+\angle CDP$.
As we know, $\angle BCP=2x\text{ and }\angle CPD=x$ so we get:
$2x=x+\angle CPD\Rightarrow \angle CPD=2x-x\Rightarrow \angle CPD=x$.
Hence in the triangle $\Delta CPD$, $\angle CPD=\angle CDP=x$.
As we know, from the converse of the isosceles triangle property, sides corresponding to equal angles are also equal. Therefore, CP = CD. Hence proved.
(ii) Now let us prove DP bisects $\angle CDQ$.
Hence we need to prove $\angle CDP=\angle PDQ$.
From the diagram, we know that CP || DQ.
Since CP and DQ are parallel lines and CD acts as transversal, so $\angle PCB\text{ and }\angle QDC$ will form a pair of corresponding angles. As we know, corresponding angles are always equal, therefore $\angle PCB=\angle QDC$.
As equivalent earlier, $\angle PCB=2x$ so, $\angle QDC=2x$.
Now, as we can see, $\angle PDC+\angle QDP=\angle QDC$ so $\angle PDC+\angle QDP=2x$.
Also we know $\angle PDC=x$ so,
$x+\angle QDP=2x\Rightarrow \angle QDP=2x-x\Rightarrow \angle QDP=x$.
Now $\angle QDP=\angle CDP$ therefore DP bisects $\angle CDQ$. Hence proved.

Note: Students should know all the properties of triangles before solving these sums. While using exterior angle property, make sure to take the sum of opposite interior angles only. We can take $\angle QDP=\angle CPD$ by considering PD as transversal for parallel lines PC and DQ where $\angle QPD\text{ and }\angle CPD$ are alternate interior angles.