Question

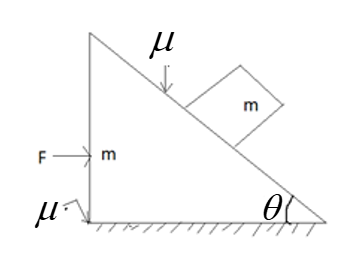
In the situation shown in figure, a wedge of mass \[m\] is placed on a rough surface, on which a block of equal mass is placed on the inclined plane of wedge. The friction coefficient between the wedge and the block and also between the ground and the wedge is\[\mu \]. An external force F is applied horizontally on the wedge towards the right, assuming the block does not slide on the wedge. Find the momentum value of force F at which the block will start slipping

Answer 1

Hint: Force accelerates the body at rest and it tends the object to come at rest when it accelerates. Hence the force is the product of mass and acceleration. The net force is the total amount of forces acting on a body.There are many forces acting on a body if it is in motion or at rest. When the body is in motion, the frictional force is one of the forces acting on a body. This frictional force is the resistive force acting on a body in motion. It makes the body come to rest.

Formula used:
\[F = ma\]
Where
\[F = \] force
\[m = \] mass
\[a = \] acceleration

Complete step by step answer:
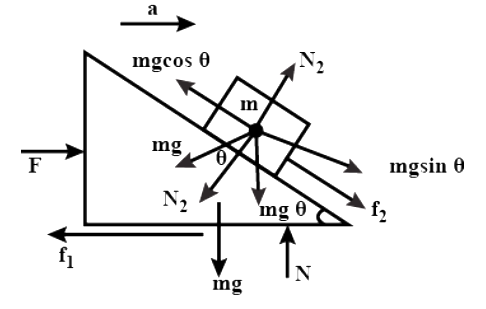
(i) Consider the block of mass \[m\] which is under force \[F\] . This force causes the block with the same mass \[m\] to move with acceleration \[a\] . And there is a frictional force acting in between the ground and the block equals \[{f_1}\]. The frictional force \[{f_1} = \mu (mg + mg) \Rightarrow 2\mu mg\]

(ii) We know that the force \[F = mg = ma\]. Both forces \[F\] and \[{f_1}\] are acting opposite to each other.
\[\therefore F - {f_1} = ma - ( - ma)\]
\[F - {f_1} = (m + m)a\]
\[a = \dfrac{{F - 2\mu mg}}{{2m}}\]

(ii) The force F is experienced by the wedge on the block. And made it to move with the same acceleration a. And there is also a frictional force is acting in between the block and the wedge equal to \[{f_2}\]

(iii) Let's consider the wedge starts moving with the acceleration a. This causes the block on the wedge to move. Therefore the force on each side of the block should be equal if we assume the block doesn’t slide.
\[\therefore ma\cos \theta = mg\sin \theta + {f_2}\]
\[ma\cos \theta = mg\sin \theta + \mu \left( {mg\cos \theta + ma\sin \theta } \right)\]
Grouping the a and g terms separately,
\[ \Rightarrow ma\cos \theta - \mu ma\sin \theta = mg\sin \theta + \mu mg\cos \theta \]
\[ \Rightarrow ma(\cos \theta - \mu \sin \theta ) = mg(\sin \theta + \mu \cos \theta )\]
\[ \Rightarrow a(\cos \theta - \mu \sin \theta ) = g(\sin \theta + \mu \cos \theta )\]
\[a = \dfrac{{g(\sin \theta + \mu \cos \theta )}}{{\left( {\cos \theta - \mu \sin \theta } \right)}}\]

Applying the value of a we find earlier in the above equation,
\[ \Rightarrow \dfrac{{F - 2\mu mg}}{{2m}} = \dfrac{{g(\sin \theta + \mu \cos \theta )}}{{(\cos \theta - \mu \sin \theta )}}\]
\[ \Rightarrow \dfrac{F}{{2m}} - \dfrac{{2\mu mg}}{{2m}} = \dfrac{{g\left( {\sin \theta + \mu \cos \theta } \right)}}{{\left( {\cos \theta - \mu \sin \theta } \right)}}\]
\[\therefore F = 2m\left[ {\mu g + \dfrac{{g\left( {\sin \theta + \mu \cos \theta } \right)}}{{\left( {\cos \theta - \mu \sin \theta } \right)}}} \right]\]
This is the value of external force which is acting on the wedge. It also causes the block to slide.

Note: (i) The force which is the result of the motion is equal to the product of mass and acceleration ma. The force which is acting on a body is equal to the product of the mass and the acceleration due to gravity mg.
(ii) The coefficient of friction \[\mu \] is the ratio of forces resisting the body to move. The rough surface is the cause of this frictional force.