Question

In the right-angle triangle \[\angle C = {90^0}\]. \[AE\] and \[BD\] are two medians of a \[\Delta ABC\] meeting at \[F\]. The ratio of the area of the \[\Delta ABF\] and the quadrilateral \[FDCE\] is
A. \[1:1\]
B. \[1:2\]
C. \[2:1\]
D. \[2 : 3\]

Answer 1

Hint: First of all, draw the diagram with the given data which will give us an idea about the problem and what we have to find. Use the properties of similar triangles to reach the solution of the given problem.

Complete step by step solution:
Given that \[\Delta ABC\] is right angled triangle at \[C\]
Given that \[BD\] is median of \[\Delta ABC\] with the base\[AC\] so, we have \[AD = CD\]
Also, \[AE\] is median of \[\Delta ABC\] with the side \[BC\]so, we have \[BE = CE\]

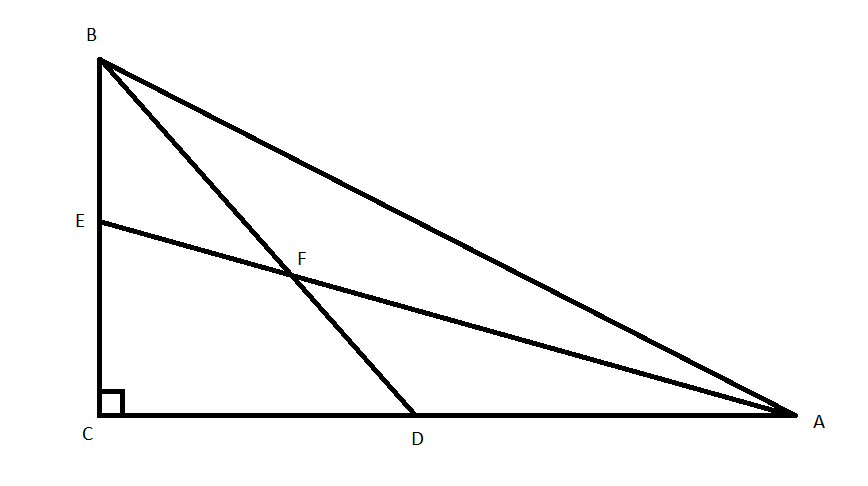
Clearly, from the figure the \[\Delta ABC,\Delta BDA\& \Delta BCD\] has same height and their bases are related as
\[\dfrac{{AC}}{2} = CD = AD\]
Hence, area of \[\Delta BCD\] = area of \[\Delta BDA\] = \[\dfrac{1}{2}\] area of \[\Delta ABC\]
Similarly, area of \[\Delta ABE\] = area of \[\Delta ACE\]= \[\dfrac{1}{2}\] area of \[\Delta ABC\]
So, area of \[\Delta BCD\] = area of \[\Delta ACE\]
\[ \Rightarrow \] area of \[FDCE\] + area of \[\Delta BEF\] = area of \[FDCE\] + area of \[\Delta AFD\]
Therefore, area of \[\Delta BEF\] = area of \[\Delta AFD\]
We know that, area of \[\Delta BCD\] = area of \[\Delta BDA\]
\[ \Rightarrow \] area of \[FDCE\] + area of \[\Delta BEF\] = area of \[\Delta AFB\] + area of \[\Delta AFD\]
Therefore, area of \[FDCE\] = area of \[\Delta AFB\]
Hence the ratio of the area of \[\Delta AFB\] to the area of quadrilateral \[FDCE\] is \[1:1\].
Thus, the correct option is A. \[1:1\]

Note: The median of a triangle cuts the base into two equal parts in length. A triangle's height is the length perpendicular line segment originating on a side and intersecting the opposite angle. If the height and base of two triangles are equal then their areas are also equal.