Question

In the right angled triangle, prove that the hypotenuse is the longest side.

Answer 1

Hint: To solve this question we need to know about the right angled triangle. So the right answer is basically a kind of triangle that has one of its interior angles equal to 90 degree or one of the angles is a right angle. While hypotenuse is the longest side in a right angle triangle having formula as $c=\sqrt{{{a}^{2}}+{{b}^{2}}}$ where “c” is the hypotenuse and the two sides are namely “a” and “b” this is the formula as per the Pythagoras Theorem.

Complete step by step answer:
The question asks us to prove that the hypotenuse is the longest in a right angled triangle. For proving this consider a triangle named $\vartriangle ABC$ where angle $B$ is the right angle which means angle $B$ is equal to 90 degree. The triangle is shown below for better understanding.

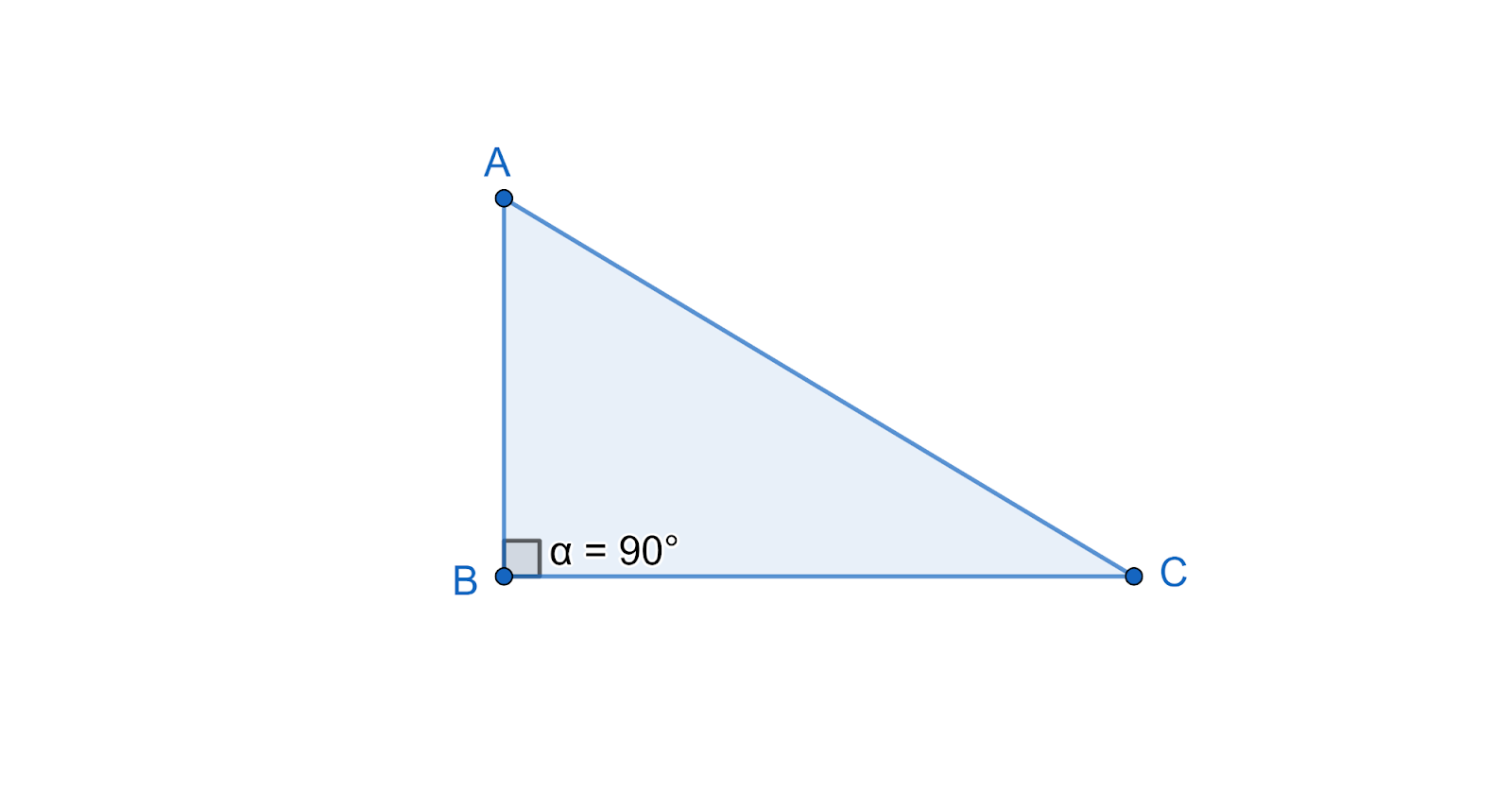
Mathematically written as:
$\angle ABC={{90}^{\circ }}$
On seeing the relation between the angles $\angle BAC$ and $\angle ABC$ we see that the $\angle BAC$ is smaller than other angle $\angle ABC$, which means:
$\Rightarrow \angle BAC < \angle ABC$
Since the rule says that the side opposite to the greater angle is bigger, which infer that
$\Rightarrow BC < AC$
Similarly, on seeing the relation between the angles $\angle ACB$ and $\angle ABC$ we see that the $\angle ACB$ is smaller than other angle $\angle ABC$, which means:
$\Rightarrow \angle ACB < \angle ABC$
Since the rule says that the side opposite to the greater angle is bigger, which infer that
$\Rightarrow AB < AC$
On analysing the above two equations we can infer that the side $AC$ is greater than the other two sides. On writing it mathematically we get:
$\Rightarrow AC > AB$ and $AC > BC$
Hence, proved that the hypotenuse is the longest side in a right angled triangle.

Note: As per the Pythagoras theorem the square of the hypotenuse is the sum of the square of the two sides in a right angled triangle. Mathematically it is written as
$\text{Hypotenuse}^{2}=\text{Perpendicular}^{2}+\text{Base}^{2}$