Question

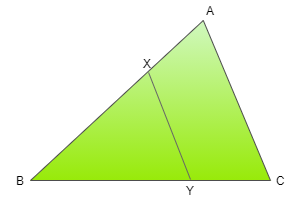
In the given figure, $XY||AC$and XY divides triangular region ABC into two parts equal in area. Determine $\dfrac{{AX}}{{AB}}$

Answer 1

Hint: To approach these types of question one should have prior knowledge about the triangles and its properties and also remember to use Area of AXYC = Area of BXY and to determine the value of $\dfrac{{AX}}{{AB}}$ show that $\Delta ABC \cong \Delta BXY$.

Complete step-by-step answer:
Now we have to find $\dfrac{{AX}}{{BX}}$
Since it is given that XY divides triangle into two equal parts
Therefore, Area of AXYC = Area of BXY (equation 1)
So, adding Area BXY to both sides of equation 1 we get
Area of AXYC + Area of BXY = 2Area of BXY
Now from figure above it is clear that Area of AXYC + Area of BXY = Area of ABC (equation 2)
Using equation (1) we can write
Area of ABC = 2*Area of BXY
So, we can say that
$\dfrac{{Area\ of {\text{ }}ABC}}{{Area\ of {\text{ }}BXY}} = 2$ (equation3)
Consider $\Delta ABC$ and $\Delta BXY$
$\angle XBY = \angle ABC$ (Common angle)
$\angle BXY = \angle BAC$ (Corresponding angle of XY||AC)
$\angle BYX = \angle BCA$ (Corresponding angle of XY||AC)
Clearly by (AAA postulate) we can say that $\Delta ABC \cong \Delta BXY$
Now using similar triangle property
By equation 3 $\dfrac{{Area\ of {\text{ }}ABC}}{{Area\ of{\text{ }}BXY}} = \dfrac{{A{B^2}}}{{B{X^2}}}{\text{ = 2}}$
So, $\dfrac{{AB}}{{BX}} = \sqrt 2 $ Or $AB = \sqrt 2 BX$
Now AB can be written as AX+XB
So, $AX + XB = \sqrt 2 XB$
So, $AX = \left( {\sqrt 2 - 1} \right)XB$
Hence the value of $\dfrac{{AX}}{{XB}} = \dfrac{{\left( {\sqrt 2 - 1} \right)}}{1}$

Note: To solve such problems we try to prove the triangles congruent using the properties Angle-Angle-Angle (AAA), Side-Angle-Side (SAS), Angle-Angle-Side (ASA) and Side-Side-Side (SSS) where these properties show that whenever the corresponding sides and their corresponding angles are equal in dimensions then the two triangles are said to be congruent.