Question

In the given figure, x equals

$\left( A \right)\dfrac{{ab}}{{a + c}}$
$\left( B \right)\dfrac{{ac}}{{a + b}}$
$\left( C \right)\dfrac{{ac}}{{b + c}}$
$\left( D \right)\dfrac{{ab}}{{b + c}}$

Answer 1

Hint: In this particular question use the concept that if we prove that the triangles LKM and OKN are similar to each other then we easily calculate the length of ON, by using property of similar triangles so use these concepts to reach the solution of the question.

Complete step by step answer:
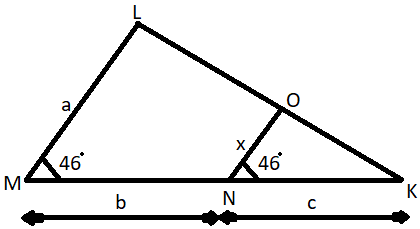
In the given figure,
LM = a, MN = b, and NK = c
$\angle LMK = \angle ONK = {46^o}$
LM||ON, therefore, $\angle MLK = \angle NOK$ (corresponding angles)
And ON = x
Now we have to find the value of x.
Now in triangle LKM and triangle OKN we have,
$\angle LMK = \angle ONK = {46^o}$ (Given angle)
$\angle LKM = \angle OKN$ (Common angle)
$\angle MLK = \angle NOK$ (Since LM||ON)
Therefore, by AAA congruence triangle LKM is similar to triangle OKN.
I.e. both the triangles are concurrent.
$ \Rightarrow \Delta LKM \sim \Delta OKN$
Now as we know that in similar triangles the ratio of the corresponding sides are equal.
Therefore, $\dfrac{{LM}}{{ON}} = \dfrac{{LK}}{{OK}} = \dfrac{{MK}}{{NK}}$
$ \Rightarrow \dfrac{{LM}}{{ON}} = \dfrac{{MK}}{{NK}}$
$ \Rightarrow \dfrac{{LM}}{{ON}} = \dfrac{{MN + NK}}{{NK}}$
Now substitute the values in the above equation we have,
$ \Rightarrow \dfrac{a}{x} = \dfrac{{b + c}}{c}$
Now simplify we have,
$ \Rightarrow x = \dfrac{{ac}}{{b + c}}$

So, the correct answer is “Option C”.

Note: Whenever we face such types of questions the key concept we have to remember is that if two triangles are similar the ratio of their corresponding sides are equal i.e. $\dfrac{{LM}}{{ON}} = \dfrac{{LK}}{{OK}} = \dfrac{{MK}}{{NK}}$, and if two lines are parallel and a third line cut these two lines then the angles made by this third line are called as corresponding angles and are equal i.e. $\angle MLK = \angle NOK$.