
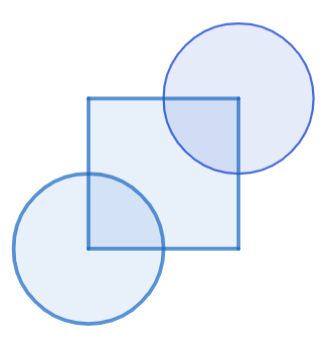
In the given figure, the side of the square is 28 cm and the radius of each circle is half of the length of the side of the square where O and O’ are centres of the circles. Find the area of the shaded region.

Answer
535k+ views
Hint: We will use formula \[\text{area of square = }{{\left( side \right)}^{2}}\] and \[area\text{ }of\text{ }circle\text{ }=\pi {{r}^{2}}\] r being the radius of circle. To find the area of the shaded region, we will find the area of the square first and then find the area of two circles and add all the areas. Finally we will subtract the area of the two quarter portion to get the area of the shaded region.
Complete step-by-step answer:
It is given in the question that the side of the square is 28cm and radius of each circle is half of the length of the side of the square where O and O’ are the centres of the circles, then we have to find the area of the shaded region.
We know that the area of the square is given by ${{\left( side \right)}^{2}}$. We know that the side of the square is 28 cm, so the area of the square will be ${{28}^{2}}=28\times 28=784c{{m}^{2}}$.
Also, we know that the area of circle is given by $\pi {{r}^{2}}$, \[radius\text{ }of\text{ }circle\text{ }=\text{ }\dfrac{side}{2}=\dfrac{28}{2}=14cm\]. So, \[area\text{ }of\text{ }circle\text{ }=\pi {{\left( 14 \right)}^{2}}=3.14\times 14\times 14=615.44c{{m}^{2}}\].
But we have two circles of equal radius, therefore an area of two circles = $2\times 615.44c{{m}^{2}}=1230.88c{{m}^{2}}$.
Now, we know that two quarters are repeating, therefore we will subtract the area of two quarters. Area of two quarters = $2\times \dfrac{615.44}{4}=\dfrac{615.44}{2}=307.72c{{m}^{2}}$.
Thus, the area of shaded region becomes = area of square + area of 2 circles - area of two quarters, putting the values, we get
$Area=\left( 784+1230.88-307.72 \right)c{{m}^{2}}=1707.16c{{m}^{2}}$.
Therefore, the area of the shaded region will be 1707.16$c{{m}^{2}}$.
Note: Students may skip or subtract the area of the two quarters from the sum of the area of the quarters from the sum of the area of square and the two circles. It is necessary to subtract the area of the quarter which is overlapping. If we do not subtract it, we will get two extra quarters, which is not required.
Complete step-by-step answer:
It is given in the question that the side of the square is 28cm and radius of each circle is half of the length of the side of the square where O and O’ are the centres of the circles, then we have to find the area of the shaded region.

We know that the area of the square is given by ${{\left( side \right)}^{2}}$. We know that the side of the square is 28 cm, so the area of the square will be ${{28}^{2}}=28\times 28=784c{{m}^{2}}$.
Also, we know that the area of circle is given by $\pi {{r}^{2}}$, \[radius\text{ }of\text{ }circle\text{ }=\text{ }\dfrac{side}{2}=\dfrac{28}{2}=14cm\]. So, \[area\text{ }of\text{ }circle\text{ }=\pi {{\left( 14 \right)}^{2}}=3.14\times 14\times 14=615.44c{{m}^{2}}\].
But we have two circles of equal radius, therefore an area of two circles = $2\times 615.44c{{m}^{2}}=1230.88c{{m}^{2}}$.
Now, we know that two quarters are repeating, therefore we will subtract the area of two quarters. Area of two quarters = $2\times \dfrac{615.44}{4}=\dfrac{615.44}{2}=307.72c{{m}^{2}}$.
Thus, the area of shaded region becomes = area of square + area of 2 circles - area of two quarters, putting the values, we get
$Area=\left( 784+1230.88-307.72 \right)c{{m}^{2}}=1707.16c{{m}^{2}}$.
Therefore, the area of the shaded region will be 1707.16$c{{m}^{2}}$.
Note: Students may skip or subtract the area of the two quarters from the sum of the area of the quarters from the sum of the area of square and the two circles. It is necessary to subtract the area of the quarter which is overlapping. If we do not subtract it, we will get two extra quarters, which is not required.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
Which country won the ICC Men's ODI World Cup in 2023?

In cricket, how many legal balls are there in a standard over?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

What does "powerplay" mean in limited-overs cricket?

What is the "Powerplay" in T20 cricket?




