Question

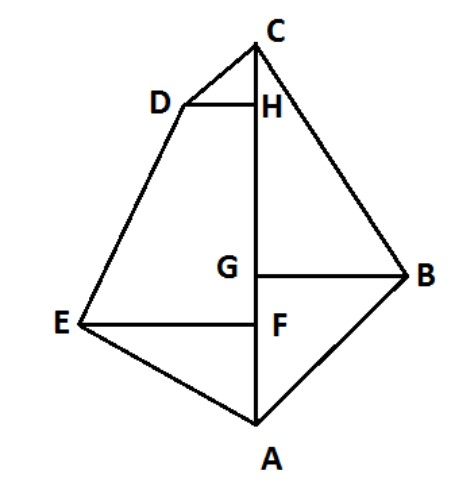
In the given figure , the measurements are : AF = $50$ m, FG = $30$ m, AH = $120$ m, CH = $30$ m, BG = $50$ m, EF = $30$ m, HD = $20$ m. Find the area of polygon ABCDE.

Answer 1

Hint:In this first observe the figure carefully and divide the polygon into different parts as AEF , DCH , ABC are the triangles we will find out the area by using formula $\dfrac{1}{2} \times $ base $ \times $ height and DH is parallel to EF hence the DHFE is trapezium we will find out its area by $\dfrac{1}{2} \times $(sum of parallel side) $ \times $ height.Adding all the calculated areas we will get required answer.

Complete step-by-step answer:
First we have to divide the polygon in different parts as AEF , DCH , ABC are the triangles .

So for the triangle ABC
Area of the triangle of ABC is $\dfrac{1}{2} \times $ base $ \times $ height .
or $\dfrac{1}{2} \times AC \times GB$
As GB is the height of triangle ABC that is equal to $50$ m .
and the AC is the base of the triangle that is equal to AC = AH + HC that is equal to $150$ m .
Hence area of triangle ABC = $\dfrac{1}{2} \times 150 \times 50$ = $3750$ ${m^2}$
Now for the triangle AEF
area of triangle is $\dfrac{1}{2} \times $ base $ \times $ height
or $\dfrac{1}{2} \times AF \times EF$
As EF is the height of triangle AEF that is equal to $30$ m it is given in the question .
and the AF is the base of triangle that is equal to $50$ m ( Given )
Hence the area of triangle AEF = $\dfrac{1}{2} \times 50 \times 30$ = $750$ ${m^2}$
Now in the triangle DHC
Area of triangle is $\dfrac{1}{2} \times DH \times HC$
Where DH and CH are given in the question that is equal to $20m$ and $30m$ respectively .
Area of triangle DHC is equal to $\dfrac{1}{2} \times 30 \times 20 = 300$ ${m^2}$
Now see the figure DHFE and DH is parallel to EF because both are perpendicular to AC .
Hence DHFC is a trapezium .
Area of Trapezium is = $\dfrac{1}{2} \times $(sum of parallel side) $ \times $height
or In DHFC it is equal to
= \[\dfrac{1}{2} \times (20 + 30) \times 70\] \[\dfrac{1}{2} \times (DH + EF) \times FH\]
It is given in the question that DH = $20$m and EF = $30$ m
And FH = AC $ - $ (CH + FA ) = $150 - (50 + 30)$
FH = $70$ m.
Area of DHFC = \[\dfrac{1}{2} \times (20 + 30) \times 70\] = $1750$ ${m^2}$
Hence the area of polygon ABCDE = Area of DHFC + Area of triangle DHC + Area of triangle AEF + Area of triangle ABC
= $1750 + 300 + 750 + 3750$ ${m^2}$
The area of polygon ABCDE = $6550$ ${m^2}$

Note:Whenever a complex figure is given to you try to break it into the simpler form as triangle , rectangle , trapezium then find out the area of each and at last add all these areas to get your answer . You can also solve this question by dividing the triangle ABC into two right angle triangles as ABF and CBF and find its area and finally add it both But it will increase your calculation and also increase the solution length .