Question

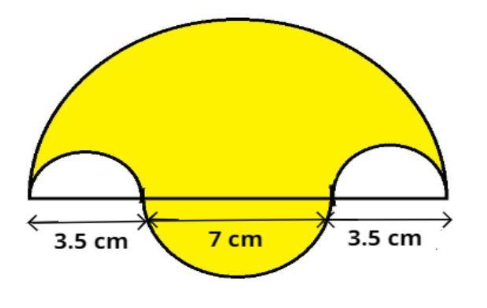
In the given figure the boundary of the shaded region consists of a semicircular and inside two semicircles and one outside of the same diameters. The diameter of the largest semicircle is 14 cm and those of smallest ones are 3.5 cm. Calculate the shaded area.

Answer 1

Hint: In this area based question we have to find the area of the shaded region. It is clear that the shaded region can easily be obtained by reducing the two smaller inside semicircles from the larger semicircle and adding this to the area of the outer smaller semicircle. Use this concept along with a basic area formula for the area of semicircles to get the answer.

Complete step-by-step answer:
As we know that the area (A) of the circle is $\pi {r^2}$ (where r is the radius of the circle).
Now as we know that diameter (d) of a circle is twice the radius.
$
   \Rightarrow d = 2r \\
   \Rightarrow r = \dfrac{d}{2} \\
 $
So substitute this value in the formula of area of circle we have
$ \Rightarrow A = \pi {\left( {\dfrac{d}{2}} \right)^2} = \pi \dfrac{{{d^2}}}{4}$
Now the area of the semi-circle (${A_1}$) is half the area of the circle.
$ \Rightarrow {A_1} = \dfrac{A}{2} = \dfrac{{\pi \dfrac{{{d^2}}}{4}}}{2} = \pi \dfrac{{{d^2}}}{8}$ Sq. unit.
Now it is given that the diameter (${D_1}$) of big shaded semicircle is 14 cm and the diameter (${D_2}$) of smaller unshaded semicircles 3.5 cm as given (see figure) so the diameter (${D_3}$) of the smaller shaded semicircle is:
Diameter of big shaded semicircle – twice multiplied by diameter of smaller unshaded semicircle.
$ \Rightarrow {D_3} = \left( {{D_1} - 2 \times {D_2}} \right) = 14 - 2 \times 3.5 = 14 - 7 = 7{\text{ cm}}$.
Now in the figure the area (${A_2}$) of the shaded region is = Area of big semi-circle having diameter 14 cm + Area of smaller semi-circle having diameter 7 cm – twice multiplied by area of semi-circle having diameter 3.5 cm.
$ \Rightarrow {A_2} = \pi \dfrac{{{{14}^2}}}{8} + \pi \dfrac{{{7^2}}}{8} - 2\pi \dfrac{{{{\left( {3.5} \right)}^2}}}{8}$
$ \Rightarrow {A_2} = \dfrac{\pi }{8}\left[ {{{14}^2} + {7^2} - 2{{\left( {3.5} \right)}^2}} \right] = \dfrac{\pi }{8}\left( {220.5} \right) = 27.5625\left( \pi \right) = \dfrac{{22}}{7}\left( {27.5625} \right) = 86.54625$ Sq. cm.

Note: Whenever we face such types of problems the key concept is to have the good understanding of the diagrammatic representation of the figure in order to figure out the required shaded region. The good gist of the basic area formula for curves like circle always helps to get on the right track to reach the answer.