Question

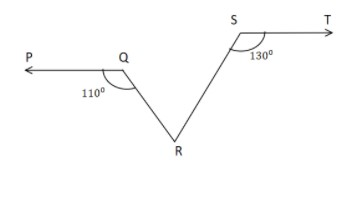
In the given figure $PQ$ is parallel to $ST$, $\angle PQR = {110^ \circ }{\text{ and }}\angle RST = {130^ \circ }$. Find $\angle QRS$.

Answer 1

Hint:In this question we have to find $\angle QRS$. So in order to solve the question we will draw a line parallel to $PQ$ and passing through the point $R$, and then by using the properties of line and angles i.e Properties of parallel lines, Sum of linear pairs of angles, we can easily solve the above question.

Complete step-by-step answer:
In the above question we are given that-
$PQ$ is parallel to $ST-----(1)$
Also,
$\angle PQR = {110^ \circ }-----(2)$
$\angle RST = {130^ \circ }-----(3)$
And according to the question we have to find $\angle QRS$.
Now in order to solve the problem firstly let’s draw a line $MN$ passing through $R$ and parallel to line $PQ$. And we are given that $PQ$ is parallel to $ST$.
Now we know that if $a\parallel b,b\parallel c, \Rightarrow a\parallel b\parallel c$

Now similarly
$MN\parallel PQ,PQ\parallel ST, \Rightarrow MN\parallel PQ\parallel ST$
So, now the above figure looks like this-

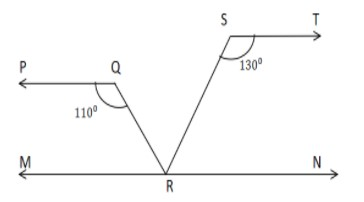
Now firstly consider parallel lines $MN{\text{ and }}PQ$ and here the transversal, which cut these two lines is $QR$.
Now by the properties of lines we know-
We know that for any two parallel lines, interior angles on the same side of the transversal are supplementary, means their sum is equal to ${180^ \circ }$.
So, for parallel lines $MN{\text{ and }}PQ$ and transversal $QR$, we get
$\angle PQR + \angle QRM = {180^ \circ }$
Now by substituting value of $\angle PQR$ from (2), we get
${110^ \circ } + \angle QRM = {180^ \circ }$
$ \Rightarrow \angle QRM = {70^ \circ }-----(4)$
Now similarly $MN{\text{ and ST}}$ are parallel lines and the transversal is $SR$.
Now again by the properties of lines we know-
We know that for any two parallel lines, interior angles on the same side of the transversal are supplementary, means their sum is equal to ${180^ \circ }$.
So, for parallel lines $MN{\text{ and ST}}$ and transversal $SR$, we get
$\angle RST + \angle SRN = {180^ \circ }$
Now substituting value of $\angle RST$ from (3), we get,
\[{130^ \circ } + \angle SRN = {180^ \circ }\]
$ \Rightarrow \angle SRN = {50^ \circ }-----(5)$
Now consider the straight lines $MN$and $\angle QRM,{\text{ }}\angle QRS,{\text{ }}\angle SRN$ are the linear pair of angles.
Now the property of sum of linear pair of angles says that-
The sum of linear pair of angles is always equal to ${180^ \circ }$.
Now using the property of linear pair of angles for the linear pair of angles $\angle QRM,{\text{ }}\angle QRS,{\text{ }}\angle SRN$, we get
$\angle QRM + \angle QRS{\text{ + }}\angle SRN = {180^ \circ }$
Now substituting values of $\angle QRM,{\text{ }}\angle SRN$ from (4), (5), we get
${70^ \circ } + \angle QRS{\text{ + 5}}{0^ \circ } = {180^ \circ }$
$ \Rightarrow \angle QRS = {60^ \circ }$
Now this is the value of the required angle.

Note:The alternative way to solve this question is-
After (4) finding value of $\angle QRM$, we can proceed like this-
Taking parallel lines \[ST\], \[MN\] and transversal line $SR$.
We know the property of parallel lines-
For any two parallel lines the corresponding angles of the transversal are equal.
So, using the above property for parallel lines \[ST\], \[MN\] and transversal line $SR$, we get
$\angle SRM = \angle RST$
Now from the figure we can say that $\angle SRM = \angle QRM + \angle QRS$, we get
$\angle QRM + \angle QRS = \angle RST$
Now substituting values from (3) and (4), we get,
${70^ \circ } + \angle QRS = {130^ \circ }$
$ \Rightarrow \angle QRS = {60^ \circ }$
So, we get required value.
Hence this is another way to solve the problem.