Question

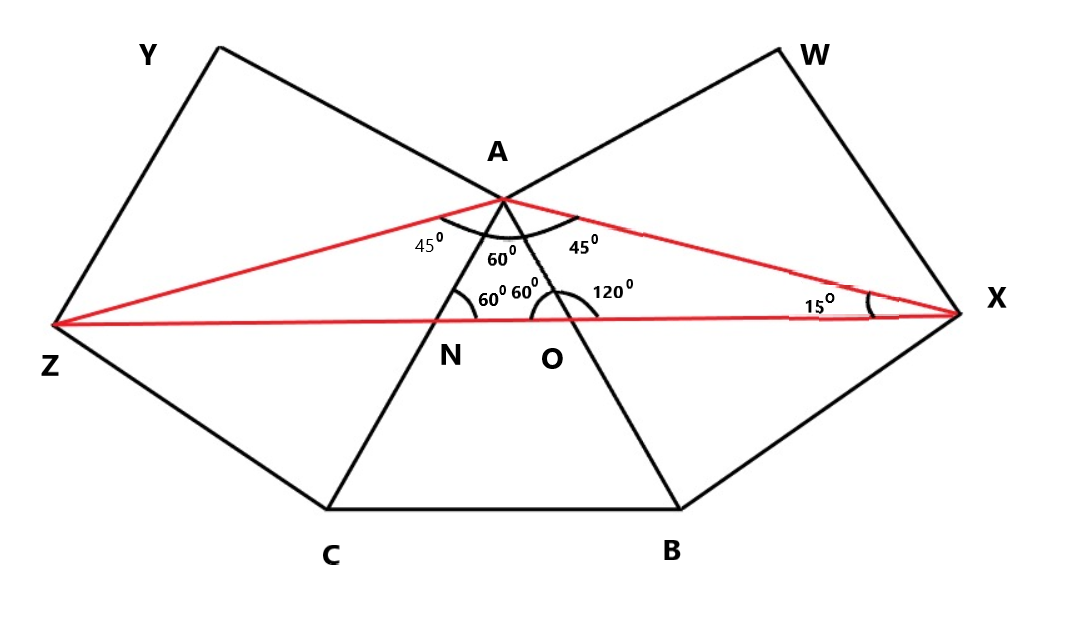
In the given figure is \[\Delta ABC\] an equilateral triangle and \[\square \text{AWXB}\] and \[\square \text{AYZE}\] are two squares. The value of \[\dfrac{1}{10}\] \[\left( \angle ZXA \right)\] is.

Answer 1

Hint: Use the properties of similar triangles.
Use the angle sum property of the triangle.

Complete step by step solution:
In the given figure \[\Delta ABC\] is an equilateral and \[\square \text{AWXB}\] and \[\square \text{AYZE}\] are two squares
\[\therefore \Delta ABC\] is equilateral therefore,
\[\angle ABC=\angle BCA=\angle BAC={{60}^{\circ }}\]
Therefore \[AX\] is the diagonal of \[\square \text{AWXB}\]
As the property of square measure of all the interior angle \[\square \text{AWXB}\]is \[{{90}^{\circ }}\]
Therefore \[\angle BAW={{90}^{\circ }}\]
The diagonal of the square are bisects the angle at the vertex
Therefore \[\angle BAX=\angle AXW=\angle DAX={{45}^{\circ }}\]
Join vertex \[X\] and \[Z\] as shown in the figure
Join \[ZX\], a straight line
Line \[ZX\] cuts the side\[AB\] and \[AC\] at equilateral triangle \[\Delta ABC\] at \[O\] and \[N\] respectively.
The smaller \[\Delta AON\] is equilateral then
\[\angle NOA=\angle NAO=\angle ONA={{60}^{\circ }}\]
Line \[AO\] is cut the straight line \[XZ\]
Hence
\[\angle ZOA+\angle XOA+\angle ZOX={{180}^{\circ }}\]
\[{{60}^{\circ }}+\angle XOA={{180}^{\circ }}\]
\[\begin{align}
& \angle XOA={{180}^{\circ }}-{{60}^{\circ }} \\
&\Rightarrow \angle XOA={{120}^{\circ }} \\
\end{align}\]

Consider \[\Delta ADX\] in figure here
\[\begin{align}
& \angle XOA+\angle XAO+\angle OXA={{180}^{\circ }} \\
&\Rightarrow {{120}^{\circ }}+{{45}^{\circ }}+\angle OXA={{180}^{\circ }} \\
&\Rightarrow \angle OXA={{180}^{\circ }}-{{165}^{\circ }} \\
&\therefore \angle OXA={{15}^{\circ }} \\
\end{align}\]
Therefore
\[\dfrac{1}{10}\]\[\left( \angle ZXA \right)={{15}^{\circ }}\].

Note: The application of properties of similar triangles is necessary in this type of problems. In Geometry, a triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180 degrees. This property is called the angle sum property of triangles.