Question

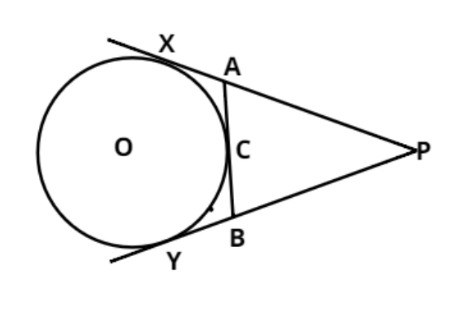
In the given figure, from an external point P, tangent PX and PY are drawn to a circle with center O. AB is another tangent to a circle at C and PX = 14cm, then find the perimeter of $\vartriangle $PAB.

Answer 1

Hint: In this question use the concept that the perimeter of a triangle is the sum of all its side. Hence the perimeter of APB is AP+BP+BA. Let AX be some variable and use it to find the value of AP as PX is known and we know that the tangents drawn from the external points onto a circle are equal in length.

Complete step-by-step answer:
From external point P, PX and PY is the tangent to the circle and it is given that PX = 14 cm.
As we know the property that from an external point the length of the tangent drawn on the circle is equal.
Therefore PX = PY = 14 cm
AX and AC are two tangents on circle from point A.
Therefore AX = AC.
Similarly, BC = BY.

Let AX = AC = x cm.
Therefore from figure AP = PX – AX
Therefore AP = (14 – x) cm.
Now AC is also x cm so the value of (AP + AC) = (14 – x + x) = 14 cm..................... (1)
So by symmetry the length of (BP + BC) = 14 cm............................ (2)

Now add equation (1) and (2) we have,
$ \Rightarrow AP + AC + BP + BC = 14 + 14 = 28$ cm.
$ \Rightarrow AP + BP + \left( {AC + BC} \right) = 28$ cm.
Now from figure (AC + BC) = AB so substitute this value in above equation we have,
$ \Rightarrow AP + BP + AB = 28$ cm............................ (3)

Now as we know that the perimeter (S) of any shape is the sum of all the sides.
Therefore the perimeter (S) of the triangle PAB is the sum of sides (AP + BP + AB).
$ \Rightarrow S = AP + BP + AB$

Now from equation (3) we have,
$ \Rightarrow S = 28$ cm.
So this is the required value of the perimeter of the triangle.
So this is the required answer.

Note: The good understanding of diagrammatic representation of the question always helps in understanding the basic geometry involved in the question. The property along with other properties of tangents to circle like a tangent never crosses a circle it just touches it and at the point of tangency the radius and the tangent are perpendicular to each other helps solving such type of problems.