Question

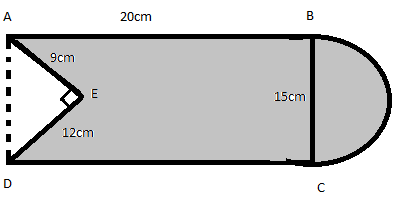
In the given figure, from a rectangle region ABCD with AB =20cm, a right triangle AED with AE = 9cm and DE = 12cm, is cut off. On the other end, taking BC = 15cm as diameter, a semicircle is added on outside the region. Find the area of the shaded region. ( use \[\pi = \dfrac{{22}}{7}\])

Answer 1

Hint :- Here we have to find the area of rectangle ABCD and the area of semicircle and the area of right-angle triangle ( i.e. AED ). And after that we have to subtract the area of the triangle from the area of the rectangle and add the area of the semicircle to the area of the rectangle to get the area of the shaded region.

Complete step by step solution:
Now let us find the area of rectangle ABCD by using the formula i.e. \[length{\text{ }} \times \;breadth\].
Here length AB = DC = 20cm and breadth BC = AD = 15cm
Area of ABCD = \[length{\text{ }} \times \;breadth\] = \[AB \times BC\] = \[20 \times 15\; = 300c{m^2}\]
Now area right-angle triangle AED = \[\dfrac{1}{2} \times base \times height\]
Area of \[\Delta AED\] = \[\dfrac{1}{2} \times AE \times ED\;\, = \dfrac{1}{2} \times 9 \times 12\; = 54c{m^2}\]
Now area of semicircle = \[\dfrac{1}{2} \times area\;of{\text{ }}circle\]
Now diameter of semicircle = 15cm so radius of semicircle = 7.5cm ( as R = \[\dfrac{D}{2}\])
So, area of semicircle = \[\dfrac{1}{2}(\pi \times {r^2})\;{\text{ = }}\;\dfrac{1}{2}(\;\dfrac{{22}}{7} \times 7.5 \times 7.5{\text{ }}){\text{ }}\]
\[ \Rightarrow \dfrac{1}{2}(\;\dfrac{{22}}{7} \times 56.25{\text{ ) = 88}}{\text{.39c}}{{\text{m}}^2}\]
Now we had to find the area of the shaded region only and because the area of the triangle is not shaded and is inscribed in the area of the rectangle we had to subtract it from the area of the rectangle.
So, now area of shaded region of rectangle = area of ABCD – area of AED
\[ \Rightarrow \]\[\;300{\text{ }}-{\text{ }}54{\text{ }} = {\text{ }}246{\text{c}}{{\text{m}}^2}\]
But the semicircle is also shaded so the area of the total shaded region = \[246{\text{c}}{{\text{m}}^2}\]+ area of the semicircle.
\[ \Rightarrow {\text{ }}246 + 88.39\; = 334.39c{m^2}\]( approx. )
Hence area of shaded region = \[334.39c{m^2}\] ( approx. )

Note :- whenever we come up with this type of problem then we must know the basic formulas ( formula for area or formula for perimeter ) of all the quadrilateral or polygon which is inscribed in the diagram. As such here we know the formula for area of rectangle ( l * b ) , triangle ( ½ * b * h ) and circle ( 1/2\[\pi \times {r^2}\]) and only then we are able to find the area for the shaded region.