Question

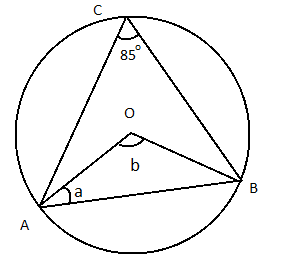
In the given figure , find the value of ‘$a$’ is

Answer 1

Hint: The angle subtended by the arc of a circle at its center is twice the angle it subtends anywhere on the circle's circumference. So we will use this theorem to find out the value of b then using property of angles of triangle we will find $a$

Complete step-by-step answer:
At center of there will be \[\angle AOB = b\]
\[ \Rightarrow \]$\angle P = \,2b$ {the angle subtended by arc of a circle at its Centre is twice the angle it subtends anywhere on the circle's circumference }
So value of b will be $\dfrac{{\angle P}}{2}\, = b$
Therefore $b = \dfrac{{{{85}^0}}}{2}$
Now in $\Delta AOB$, we have,
\[ \Rightarrow \] \[\angle AOB\] $+ \,\angle ABO\, + \,\angle BAO\, = \,{180^0}$ ……(1)
But OA =OB {radii of same circle}
We know that when two sides are equal angles opposite to them are also equal
\[ \Rightarrow \]$\angle ABO\, = \,\angle BAO$
Substituting $\angle ABO\, = \,\angle BAO$ in (1)
\[ \Rightarrow \]$\angle AOB\, + \,\angle BAO\, + \,\angle BAO\, = \,{180^0}$
\[ \Rightarrow \]$\angle AOB\, + 2\,\angle BAO\, = \,{180^0}$
\[ \Rightarrow \]$\dfrac{{{{85}^0}}}{2}\, + \,2(a)\, = {180^0}$
On simplifying, we get
\[ \Rightarrow \] \[2a{\text{ }} = {\text{ }}\left( {{{360}^0}-{\text{ }}{{85}^0}} \right)/2\]
\[ \Rightarrow \] \[2a = \dfrac{{({{360}^0} - {{85}^0})}}{2}\]
Now, we have
\[ \Rightarrow \]$4a = 275$
Therefore
\[ \Rightarrow \]\[a = \dfrac{{275}}{4} = {68.8^0}\]

Hence we have calculated value of $a = {68.8^0}$

Note: In this question you may get confused regarding calculation of value of $a$ one may apply the theorem in converse form and substitute \[\angle P\] = \[\dfrac{b}{2}\] this is not correct.
Remember all theorems related to circles if you know the theorem it becomes very easy for you to get your answers and it will also give the correct answer otherwise you might commit a mistake with the wrong approach. You should keep in mind what the statement of the theorem is and how to use it.
You can also solve this question by first equating the angles to make it an isosceles triangle using radius the two sides of the triangle will become equal and then finding out the relationship between angles then substituting values of angles and using properties of triangles and theorems on circle proceed.