Question

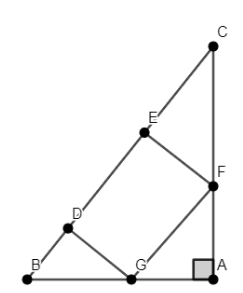
In the given figure, DEFG is a square and \[\angle BAC={{90}^{\circ }}\]. Show that \[D{{E}^{2}}=BD\times EC\].

Answer 1

Hint: Prove that $\Delta BDG$ and $\Delta ECF$ are similar using AA (Angle – Angle) Property. Use the fact that the ratio of corresponding sides of similar triangles is equal. Rearrange the terms to prove the given expression.

Complete step-by-step solution -
We have $\Delta ABC$ with a square DEFG inscribed in it such that \[\angle BAC={{90}^{\circ }}\]. We have to prove that \[D{{E}^{2}}=BD\times EC\].

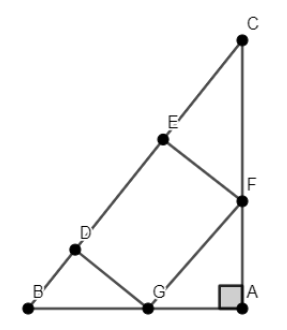
We will prove that $\Delta BDG$ and $\Delta ECF$ are similar.
As DEFG is a square, each angle is equal to ${{90}^{\circ }}$. Thus, we have $\angle GDE=\angle DEF={{90}^{\circ }}$.
We observe that $\angle GDE$ and $\angle BDG$ form a linear pair. Thus, we have $\angle GDE+\angle BDG={{180}^{\circ }}$.
$\Rightarrow {{90}^{\circ }}+\angle BDG={{180}^{\circ }}\Rightarrow \angle BDG={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$
Similarly, we observe that $\angle DEF$ and $\angle CEF$ form a linear pair. Thus, we have $\angle DEF+\angle CEF={{180}^{\circ }}$.
$\Rightarrow {{90}^{\circ }}+\angle CEF={{180}^{\circ }}\Rightarrow \angle CEF={{180}^{\circ }}-{{90}^{\circ }}={{90}^{\circ }}$
Thus, we have $\angle CEF=\angle BDG={{90}^{\circ }}.....\left( 1 \right)$.
Let’s assume that $\angle DBG=x$.
We know that the sum of all interior angles of a triangle is ${{180}^{\circ }}$.
In $\Delta BDG$, we have $\angle BDG+\angle DGB+\angle GBD={{180}^{\circ }}$.
Substituting the values $\angle GBD=x,\angle BDG={{90}^{\circ }}$ in the above equation, we have $x+{{90}^{\circ }}+\angle DGB={{180}^{\circ }}$.
Rearranging the terms, we have $\angle DGB={{180}^{\circ }}-x-{{90}^{\circ }}={{90}^{\circ }}-x$.
We know that $\angle DGF={{90}^{\circ }}$ as all the angles of a square measure ${{90}^{\circ }}$.
As BA is a straight line, we have $\angle BGD+\angle DGF+\angle FGA={{180}^{\circ }}$.
Substituting $\angle DGF={{90}^{\circ }},\angle BGD={{90}^{\circ }}-x$ in the above equation, we have ${{90}^{\circ }}+{{90}^{\circ }}-x+\angle FGA={{180}^{\circ }}$.
Rearranging the terms, we have $\angle FGA={{180}^{\circ }}-\left( {{90}^{\circ }}+{{90}^{\circ }}-x \right)=x$.
We know that sum of all interior angles of a triangle is ${{180}^{\circ }}$ and $\angle GAF={{90}^{\circ }}$ as $\Delta GAF$ is a right-angled triangle, right-angled at A.
Thus, we have $\angle FGA+\angle GAF+\angle AFG={{180}^{\circ }}$.
Substituting $\angle FGA=x,\angle GAF={{90}^{\circ }}$ in the above equation, we have $x+{{90}^{\circ }}+\angle AFG={{180}^{\circ }}$.
Rearranging the terms, we have $\angle AFG={{180}^{\circ }}-{{90}^{\circ }}-x={{90}^{\circ }}-x$.
We know that $\angle GFE={{90}^{\circ }}$ as all the angles of a square measure ${{90}^{\circ }}$.
As AC is a straight line, we have $\angle AFG+\angle GFE+\angle EFC={{180}^{\circ }}$.
Substituting $\angle GFE={{90}^{\circ }},\angle AFG={{90}^{\circ }}-x$ in the above equation, we have ${{90}^{\circ }}+{{90}^{\circ }}-x+\angle EFC={{180}^{\circ }}$.
Rearranging the terms, we have $\angle EFC={{180}^{\circ }}-\left( {{90}^{\circ }}+{{90}^{\circ }}-x \right)=x$.
Thus, we observe that $\angle DBG=\angle EFC=x.....\left( 2 \right)$.
Using equation (1) and (2), we observe that two angles of the triangles $\Delta BDG$ and $\Delta FEC$ are equal.
Thus, using AA (Angle – Angle) Property, we observe that $\Delta BDG$ and $\Delta FEC$ are similar.
We know that the ratio of corresponding sides of similar triangles is equal.
Thus, we have $\dfrac{BD}{FE}=\dfrac{DG}{EC}=\dfrac{BG}{FC}.....\left( 3 \right)$.
As DEFG is a square, the length of all of its sides is equal. Thus, we have $DE=EF=FG=GD.....\left( 4 \right)$.
Substituting equation (4) in equation (3), we have $\dfrac{BD}{DE}=\dfrac{DE}{EC}$.
Cross multiplying the terms of the above equation, we have $BD\times EC={{\left( DE \right)}^{2}}$.
Hence, we have proved that $BD\times EC={{\left( DE \right)}^{2}}$.

Note: We can also solve this question by proving that $\Delta BDG$ and $\Delta GAF$ are similar. Also, prove that $\Delta GAF$ is similar to $\Delta FEC$ and thus $\Delta BDG$ is similar to $\Delta FEC$. We can also prove that the two triangles are similar using AAA Property.