
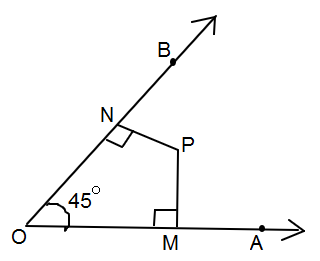
In the given figure, $\angle AOB = 45^\circ $, $PM \bot OA$ and $PN \bot OB$, find the measure of $\angle MPN$.

Answer
574.5k+ views
Hint: consider all the given details in the question, it leads to the solution.
In a closed figure, we can use Sum of interior angles of a polygon of side n, if all the angles are known except one.
Complete step by step solution:
Given,
$PM \bot OA$
$ \Rightarrow \angle PNO = 90^\circ $ …… (1)
$PN \bot OB$
$ \Rightarrow \angle PMO = 90^\circ $ …… (2)
$\angle AOB = 45^\circ = \angle MON$ …… (3)
From the figure, it can be seen angle $\angle MPN$ is a part of a closed figure with
Vertices M, P, N, O forms a quadrilateral.
Quadrilateral of sides MP, NP, NO. MO,
$\because $number of sides, n = 4
Key rule: Sum of interior angles of a polygon of side n, is given by:
$(n - 2) \times 180^\circ $, where $n$ is numbers of side of polygon
Sum of all interior angles of quadrilateral MPNO = $(n - 2) \times 180^\circ $
$ = (4 - 2) \times 180^\circ $
$ = 2 \times 180^\circ $
$ = 360^\circ $ …… (4)
Also, we know
Sum of all interior angles of quadrilateral MPNO:
$\angle PMO + \angle MPN + \angle PNO + \angle MON = 360^\circ $
$90^\circ + \angle MPN + 90^\circ + 45^\circ = 360^\circ $ (from (1) to (4))
$ \angle MPN = 360^\circ - 225^\circ \\
{\text{ }} = 135^\circ \\ $
The required angle $\angle MPN{\text{ is }}135^\circ $.
Note:
Vertex is a plural of the vertex (many vertexes).
The above result: the sum of all interior angles of a quadrilateral is $360^\circ $: can be learnt as it is.
Hence, the sum of all interior angles of square is $360^\circ $, and of the rectangle is also $360^\circ $.
Similarly, for all the quadrilateral namely, rhombus, trapezium, their sum of all interior angles is $360^\circ $.
In a closed figure, we can use Sum of interior angles of a polygon of side n, if all the angles are known except one.
Complete step by step solution:
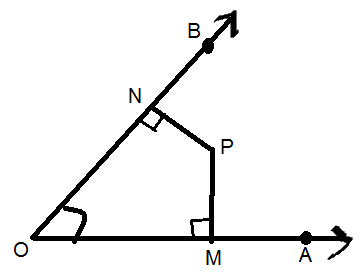
Given,

$PM \bot OA$
$ \Rightarrow \angle PNO = 90^\circ $ …… (1)
$PN \bot OB$
$ \Rightarrow \angle PMO = 90^\circ $ …… (2)
$\angle AOB = 45^\circ = \angle MON$ …… (3)
From the figure, it can be seen angle $\angle MPN$ is a part of a closed figure with
Vertices M, P, N, O forms a quadrilateral.
Quadrilateral of sides MP, NP, NO. MO,
$\because $number of sides, n = 4
Key rule: Sum of interior angles of a polygon of side n, is given by:
$(n - 2) \times 180^\circ $, where $n$ is numbers of side of polygon
Sum of all interior angles of quadrilateral MPNO = $(n - 2) \times 180^\circ $
$ = (4 - 2) \times 180^\circ $
$ = 2 \times 180^\circ $
$ = 360^\circ $ …… (4)
Also, we know
Sum of all interior angles of quadrilateral MPNO:
$\angle PMO + \angle MPN + \angle PNO + \angle MON = 360^\circ $
$90^\circ + \angle MPN + 90^\circ + 45^\circ = 360^\circ $ (from (1) to (4))
$ \angle MPN = 360^\circ - 225^\circ \\
{\text{ }} = 135^\circ \\ $
The required angle $\angle MPN{\text{ is }}135^\circ $.
Note:
Vertex is a plural of the vertex (many vertexes).
The above result: the sum of all interior angles of a quadrilateral is $360^\circ $: can be learnt as it is.
Hence, the sum of all interior angles of square is $360^\circ $, and of the rectangle is also $360^\circ $.
Similarly, for all the quadrilateral namely, rhombus, trapezium, their sum of all interior angles is $360^\circ $.
Recently Updated Pages
Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Convert 200 Million dollars in rupees class 7 maths CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

Repeated addition of the same number is called a addition class 7 maths CBSE





