Question

In the given figure, $\angle ABD=\angle BDC$ and $CD=4AB$ . Show that $BD=5BE$ .

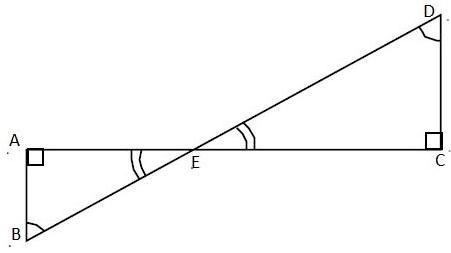
Answer 1

Hint: For solving this question first we will prove that the two right-angle triangles shown in the figure are similar. Then, using the properties of similar triangles and with the help of the given data, we will prove the result.

Complete step-by-step answer:
In the figure below, $\angle ABD=\angle BDC$ and $CD=4AB$ .

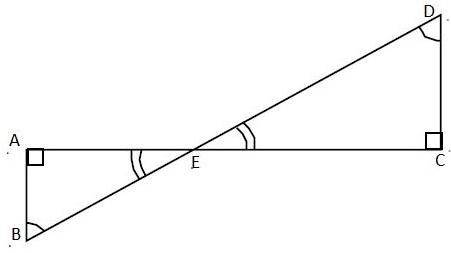
Before we solve the question first we should know two important properties of triangles and they are:
1. Sum of interior angles of a triangle is ${{180}^{0}}$ . And when two different angles of any two triangles are equal then the third angle will be automatically equal, or we can say that all 3 angles of the two triangles will be equal.
2. Now, if all three angles of two triangles are equal then, the triangles will be similar to each other. Then, the ratio of their corresponding sides will be equal.
Now, we come back to our question. In the given figure we can say that,
$\begin{align}
  & \angle ABD=\angle BDC\text{ }\left( \text{Given} \right) \\
 & \text{Then, }\angle ABE=\angle CDE \\
 & \text{And, }\angle AEB=\angle CEB\text{ }\left( \text{Vertically opposite angles} \right) \\
\end{align}$
Thus, now consider $\Delta AEB$ and $\Delta CED$ . In these triangles, we can write using the above data,
$\begin{align}
  & \angle ABE=\angle CDE \\
 & \text{ }\angle AEB=\angle CEB \\
 & \text{And, }\angle EAB=\angle ECD \\
 & \text{Then, }\Delta AEB\approx \Delta CED \\
\end{align}$
Now, as we have proved that $\Delta AEB$ and $\Delta CED$ are similar to each other. So, the ratio of corresponding sides will be equal. Then,
$\dfrac{AE}{CE}=\dfrac{BE}{DE}=\dfrac{AB}{CD}$
Now, it is given that $CD=4AB$ . So, substitute $CD=4AB$ in the above equation. Then,
$\dfrac{AE}{CE}=\dfrac{BE}{DE}=\dfrac{1}{4}$
Now, from the above equation, we can write that $DE=4BE$ . And it is obvious that $BD=BE+DE$ . Then,
$\begin{align}
 & \Rightarrow BD=BE+4BE \\
 & \Rightarrow BD=5BE \\
\end{align}$
Thus, from the above result, we can say that $BD=5BE$ .
Hence, proved.

Note: Here, the student should correctly apply the properties of triangles and proceed stepwise to solve the question. Moreover, be careful in writing the name of similar triangles. For example in this question we cannot write that $\Delta ABE\approx \Delta CED$ , the correct way is $\Delta ABE\approx \Delta CDE$ .