Question

In the given figure $\angle 1=\angle 2\,and\,\Delta NSQ\cong \Delta MTR$, then prove that $\Delta PTS\sim \Delta PRQ$.

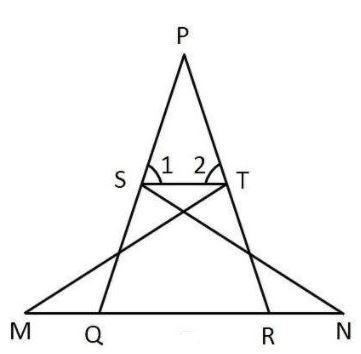
Answer 1

Hint: We have to prove that $\Delta PTS\sim \Delta PRQ$, so to do this first we will prove that \[\angle NQS=\angle MRT\] using the property of CPCT as we are given that $\Delta NSQ\cong \Delta MTR$. After that, we will apply the angle sum property in both the triangles PST and QPR, and from that, we will get the value of $\angle PQR$ equal to the $\angle PST$ and also $\angle P$ is common. So by the property of AA similarity, we will prove both the triangles similar to each other.

Complete step by step answer:
We are given that,
$\begin{align}
  & \angle 1=\angle 2\,, \\
 & \Delta NSQ\cong \Delta MTR \\
\end{align}$
And we have to prove that,
$\Delta PTS\sim \Delta PRQ$

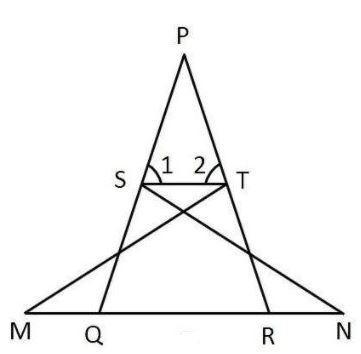
We know that if two triangles are congruent to each other then their all angles and all sides are also congruent to each other and this property is known as corresponding parts of congruent triangles i.e. CPCT.

As it is given that $\Delta NSQ\cong \Delta MTR$ so using CPCT we get,
$\angle NSQ=\angle MRT$
i.e.
$\angle PQR=\angle PRQ\,\,\,\,....\left( 1 \right)$
Now we also know that the sum of all the three internal angles of the triangles is ${{180}^{\circ }}$ and this property is known as angle sum property of triangles.
So using the angle sum property in $\Delta PST$, we get
$\angle P+\angle 1+\angle 2={{180}^{\circ }}$
Since it is given that $\angle 1=\angle 2$, so we get
\[\begin{align}
  & \angle P+\angle 1+\angle 1={{180}^{\circ }} \\
 & \angle P+2\angle 1={{180}^{\circ }}\,\,\,\,.....\left( 2 \right) \\
\end{align}\]
Similarly applying angle sum property in $\Delta PQR$, we get
\[\angle P+\angle PQR+\angle PRQ={{180}^{\circ }}\]
From equation 1 we have \[\angle PQR=\angle PRQ\], so we get
\[\angle P+\angle PQR+\angle PQR={{180}^{\circ }}\]
\[\angle P+2\angle PQR={{180}^{\circ }}\,\,\,....\left( 3 \right)\]
As we can see that RHS of both the equations 2 and 3 are equal so by equation their LHS we get,
\[\angle P+2\angle 1=\angle P+2\angle PQR\]
$\begin{align}
  & 2\angle 1=2\angle PQR \\
 & \angle 1=\angle PQR\,\,\,\,.....\left( 4 \right) \\
\end{align}$
So now in the $\Delta PTS\,\,and\,\,\Delta PRQ$ we have,
\[\begin{align}
  & \angle P=\angle P\,\,\,\,\,\,\left( \operatorname{common}\,\,angle \right) \\
 & \angle PST=\angle PQR\,\,\,\,\left( \operatorname{From}\,\,4 \right) \\
\end{align}\]
Hence using AA similarity property we can say that,
$\Delta PTS\sim \Delta PRQ$
Hence proved.

Note:
 To solve problems related to geometry try to solve it step by step because these kinds of problems are generally asked in the subjective type pattern and you may lose marks if you skip any step. And also remember and revise all the mentioned properties in the solution it will help you solve these kinds of problems faster.