Question

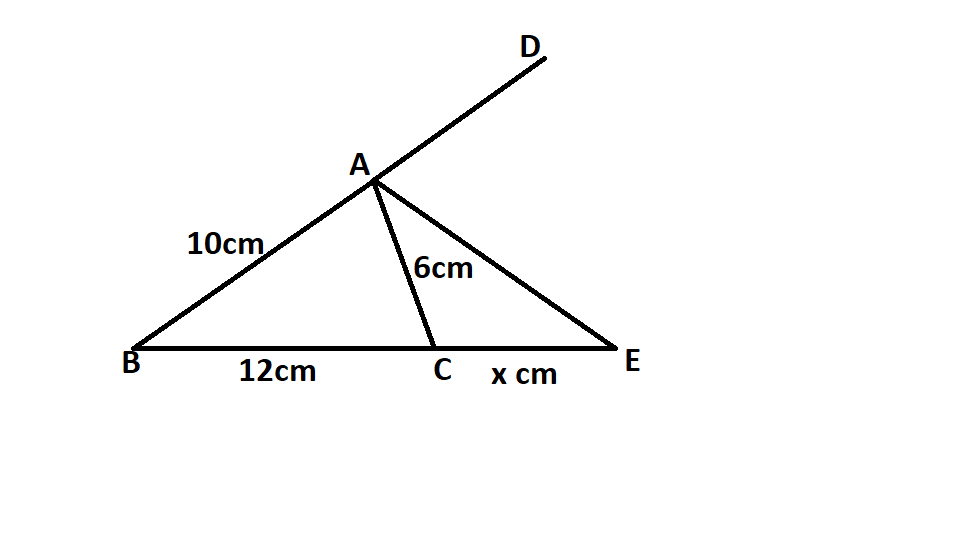
In the given figure, AE is the bisector of the exterior $\angle CAD$ meeting BC produced in E. If AB = 10 cm, AC = 6 cm and BC = 10 cm. Find CE.

Answer 1

Hint: This question can be solved using the Sine rule. It relates the length of sides and the sine of angles of a triangle. According to the law, $\dfrac{a}{\sin A}=\dfrac{b}{\operatorname{sinB}}=\dfrac{c}{\operatorname{sinC}}=d$.

Complete step-by-step answer:
Consider the figure given in the question. We need to calculate the length of CE which is a side of the triangle ACE.

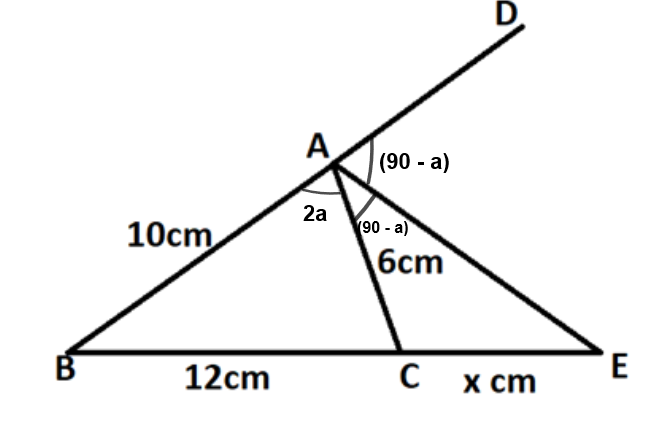
Now to find the length of CE, we will assume that $\angle BAC=2a$.
We know that a linear pair of angles sum up to 180 degrees, a linear pair of angles are supplementary.
So, here we can see in the figure that AB is a line and hence,
$\begin{align}
  & \angle BAC+\angle CAD=180 \\
 & 2a+\angle CAD=180 \\
\end{align}$
Since we have substituted the value of $\angle BAC=2a$.
$\angle CAD=180-2a....\left( i \right)$
Now, it is given in the question that AE is the bisector of $\angle CAD$ so it means that it will divide the triangle angle DAC into two equal parts i.e. $\angle CAE=\angle DAE$
So using equation (i)
$\angle CAE=\angle DAE=\dfrac{1}{2}\angle CAD=90-a$
Now we will use the sine rule.

Sine rule is an equation relating the length of sides of a triangle to the sines of its angles. According to the law, $\dfrac{a}{\sin A}=\dfrac{b}{\operatorname{sinB}}=\dfrac{c}{\operatorname{sinC}}=d$.
So, in triangle ABE in the given figure,
$\begin{align}
  & \angle BAE=2a+90-a \\
 & \angle BAE=90+a \\
\end{align}$
Now we will use sine rule here in the triangle ABE and we will get,
$\dfrac{\sin (90+a)}{x+12}=\dfrac{\sin E}{10}$
We know that $\sin (90+a)=\cos a$ as $\left( 90+a \right)$ lies in the second quadrant and we know that sine is positive in II and IV quadrants.
So,
$\dfrac{\cos a}{x+12}=\dfrac{\sin E}{10}....\left( ii \right)$
In triangle ACE,
$\angle CAE=90-a$
Now in triangle ACE, we use the sine rule
$\dfrac{\sin (90-a)}{x}=\dfrac{\sin E}{6}$
We know $\sin \left( 90-a \right)=\cos a$ and $\left( 90-a \right)$ lies in the first quadrant where every trigonometric function is positive so, we get
$\dfrac{cosa}{x}=\dfrac{\sin E}{6}....\left( iii \right)$
From equation (ii) and (iii).
Dividing equation (iii) by equation (ii), we will get
$\begin{align}
  & \dfrac{10\cos a}{x+12}=\dfrac{6\cos a}{x} \\
 & 10x=6x+72 \\
 & 4x=72 \\
 & x=18 \\
\end{align}$
So $x=18cm$
So, the length of CE is 18 cm.

Note: We cannot use the trigonometric functions because trigonometric functions relate the angle of the right-angled triangle to the ratio of two side-length and here it’s not given that triangle is right-angled. Whereas we can use the sine rule of the triangle as it is valid for all types of triangles.