Question

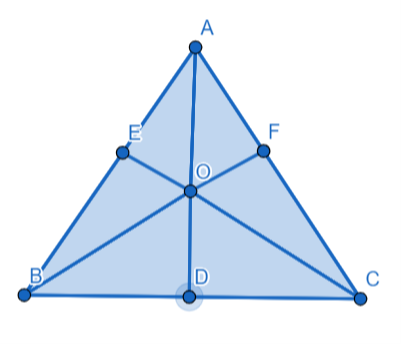
In the given figure, AD, BF and CF are medians of a triangle ABC and O is a point of concurrency of medians. If AD = 6 cm, then OD is equal to:

\[\begin{align}
  & (A)\text{ 2 cm} \\
 & \text{(B) 3 cm} \\
 & \text{(C) 4 cm} \\
 & \text{(D) }\dfrac{2}{3}cm \\
\end{align}\]

Answer 1

Hint: First of all, we have to understand the definition of median. A median that passes through a vertex divides the opposite side of the vertex into two parts. The point of concurrency of all medians is called the centroid of \[\Delta ABC\]. The centroid of \[\Delta ABC\] divided the median in the ratio of \[2:1\]. From the question, we are having the length of median AD. By using this concept, we can find the value of OD.

Complete step by step solution:
Before solving the question, we should know the definition of median and its properties. A median that passes through a vertex divides the opposite side of the vertex into two parts. The point of concurrency of all medians is called the centroid of \[\Delta ABC\]. We know that the centroid of \[\Delta ABC\] divided the median in the ratio of \[2:1\].

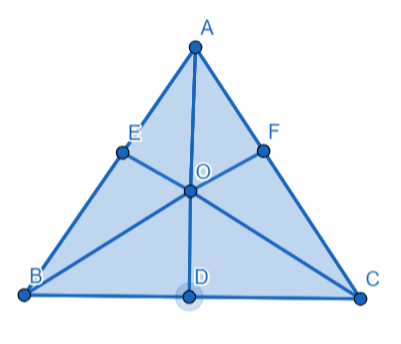
Let us assume \[\Delta ABC\] whose vertices are A, B and C respectively. Let AD, BF and CE are the medians passing through the vertices A, B and C respectively. A median pass through A divides the side BC into two equal parts. In the same way, median through vertex B divides the side AC into two equal parts. In the same way, median through vertex C divides the side AB into equal parts. Let us assume the intersection of medians AD, BF and CE be point O. This point O represents the centroid of \[\Delta ABC\]. The point O divides the line AD, BF and CF in the ratio 2:1.
So, we get
\[\begin{align}
  & AO:OD=2:1 \\
 & BO:OF=2:1 \\
 & CO:OE=2:1 \\
\end{align}\]
From the question, it was given that AD = 6 cm.
AD can be divided by point O in the ratio \[2:1\].
We get
\[\dfrac{AO}{OD}=\dfrac{2}{1}=2\]
\[\Rightarrow AO=2OD......(1)\]
From the diagram, it is clear that
\[AD=AO+OD.....(2)\]
Now we will substitute equation (2) in equation (1).
\[AD=3OD\]
We know that the length of AD is equal to 6 cm.
\[\begin{align}
  & \Rightarrow 3OD=6cm \\
 & \Rightarrow OD=2cm \\
\end{align}\]
From this it is clear that the length of OD is equal to 2 cm.
Hence, option (A) is correct.

Note: We know that the centroid divides the median in the ratio \[2:1\]. Some students may have misconceptions and they may write \[OD:AO=2:1\].
If this misconception is followed,
We get \[\dfrac{OD}{AO}=\dfrac{2}{1}\]
By using cross multiplication, we get
\[OD=2AO.....(1)\]
\[AD=AO+OD....(2)\]

 

Now we will substitute equation (1) in equation (2).
\[AD=3AO....(3)\]
From equation (3), we get
\[\begin{align}
  & \Rightarrow 3AO=6cm \\
 & \Rightarrow AO=2cm....(4) \\
\end{align}\]
Now we will substitute equation (4) in equation (2).
\[\Rightarrow OD=4cm\]
So, it is clear that this will give an incorrect answer.