Question

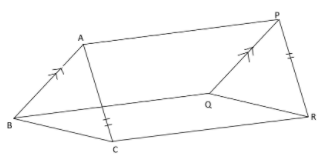
In the given figure, $AB||PQ$ and $AB = PQ$. Also, $AC||PR$ and $AC = PR$. Prove that $BC||QR$ and $BC = QR$.
     

Answer 1

Hint: A quadrilateral is said to be a parallelogram if a pair of its opposite sides are parallel and equal to each other. Find the parallelograms in the diagram, and use its properties.

Complete step-by-step answer:

     

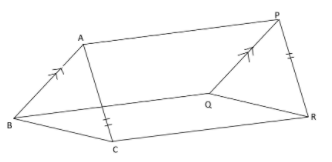
In quadrilateral ABQP,
We are given that , $AB||PQ$and $AB = PQ$.
Therefore, ABQP is a parallelogram.
(Since a pair of opposite sides are parallel as well as equal)
So, $AP||BQ$ (1)
$AP = BQ$ (2) (Both pairs of opposite sides of parallelogram are equal and parallel.)
Similarly,
In quadrilateral ACPR,
Given that $AC||PR$and $AC = PR$.
Again we can say that
ACPR is a parallelogram.
Since in a parallelogram, opposite sides are equal and parallel,
$AP = CR$ (3)
$AP||CR$ (4)
Using equations (1) and (4)
We can compare to conclude that $BQ||CR$
Comparing equation (2) and (3)
We get,
$BQ = CR$
In quadrilateral BQRC,
$
  BQ||CR \\
  BQ = CR \\
 $
Hence, proved.

Note: For solving these type of questions, try to memorize different types of properties of different quadrilaterals, so that when you fall upon these questions, you can easily recognise the type of the quadrilateral and all its properties which may help you to a great deal. Always remember to give reasons for every statement you write be it a property or given already in the question.