Question

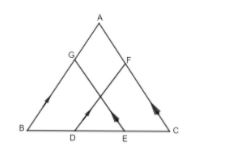
In the given figure: \[AB||FD,AC||GE,BD=CE;\] prove that
(i) BG = DF
(ii) CF = EG

Answer 1

Hint: We are asked to show that BG = DF and CF = EG. We will first show that \[\Delta GBE\cong \Delta FDC.\] To do so, we will use that corresponding angles are equal when two parallels are cut by the traversal. As, AB||FD gives us \[\angle GBE=\angle FDC\] and AC||GE gives us \[\angle GEB=\angle FCD,\] using Angle – Side – Angle (ASA) congruence rule, we have \[\Delta GBE\cong \Delta FDC\] and then using the corresponding parts.

Complete step-by-step answer:
We are given that,
\[AB||FD,AC||GE,BD=CE\]
First of all, we have,
\[BD=CE\]
Adding DE to both the sides, we get,
\[BD+DE=CE+DE\]
\[\Rightarrow BE=DC....\left( i \right)\]
Now, as AB||FD, then BE will be the traversal. So, we get,
\[\angle GBE=\angle FDC.....\left( ii \right)\left[ \text{Corresponding Angle} \right]\]
Similarly, as AC||GE and BC act as the traversal, so, we get,
\[\angle GEB=\angle FCD.....\left( iii \right)\left[ \text{Corresponding pair of angles are equal} \right]\]
Now, in triangle GBE and triangle FDC, we have,
\[\angle GBE=\angle FDC\left[ \text{Using }\left( ii \right) \right]\]
\[BE=DC\left[ \text{Using }\left( i \right) \right]\]
\[\angle GEB=\angle FCD\left[ \text{Using }\left( iii \right) \right]\]
So, by Angle – Side – Angle Congruence rule, we get that,
\[\Delta GBE\cong \Delta FDC\]
In the Congruent triangle, the corresponding parts are equal. So, we get,
BG = DF (By CPCT, as triangle GBE is congruent to triangle FDC)
GE = CF (By CPCT, as triangle GBE is congruent to triangle FDC)

Note: Students should note that adding the same quantity to both sides of the equality will not affect equality and that is why we can add DE to both sides of BD = CE. When two lines are parallel, the corresponding angles are always equal.

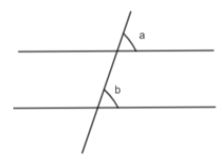
Here, angle a is equal to angle b.