Question

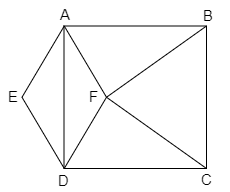
In the given figure, ABCD is a square, BCF is an equilateral triangle and AEDF is a rhombus. Find $\angle EAF$

A. $30^\circ $
B. $120^\circ $
C. $150^\circ $
D. None of these

Answer 1

Hint: From the figure, it is shown that $\angle AFB$ and $\angle CFD$ are right angles. As BCF is an equilateral triangle, so calculate $\angle BFC$. As we know that angles around a point add up to $360^\circ $. From this find the value of $\angle AFD$. From the properties of the rhombus, the sum of adjacent angles of the rhombus is supplementary. From this property, we will get the value of $\angle EAF$.

Complete step by step answer:
From the figure, it is clear that $\angle AFB$ and $\angle CFD$ is right angles. So,
$ \Rightarrow \angle AFB = \angle CFD = 90^\circ $
As BCF is an equilateral triangle, we know that all angles of an equilateral triangle are equal. Then,
$ \Rightarrow \angle BFC = 60^\circ $
Now, we know that all angles around a point add up to $360^\circ $. Thus at point F,
$ \Rightarrow \angle BFC + \angle AFB + \angle AFD + \angle CFD = 360^\circ $
Substitute the values,
$ \Rightarrow 60^\circ + 90^\circ + \angle AFD + 90^\circ = 360^\circ $
Add the terms on the left side,
$ \Rightarrow 240^\circ + \angle AFD = 360^\circ $
Move the angle value on the right side,
$ \Rightarrow \angle AFD = 360^\circ - 240^\circ $
Subtract the value on the right side,
$ \Rightarrow \angle AFD = 120^\circ $
Now, apply the property of rhombus states that the sum of adjacent angles of a rhombus is supplementary. So,
$ \Rightarrow \angle AFD + \angle EAF = 180^\circ $
Substitute the value,
$ \Rightarrow 120^\circ + \angle EAF = 180^\circ $
Move the angle value on the right side,
$ \Rightarrow \angle EAF = 180^\circ - 120^\circ $
Subtract the value on the right side,
$ \Rightarrow \angle EAF = 60^\circ $
Thus, the value of $\angle EAF$ is $60^\circ $.

Hence, option (D) is the correct answer.

Note: A square is a quadrilateral in which all the four sides are equal in length and all the angles are equal. All the angles are equal to 90 degrees i.e. they are right angles.
A rhombus is a type of quadrilateral in which all four sides are of equal length. Also, the diagonals are perpendicular to one another and bisect each other too.
A triangle whose all three sides are of equal length is called an equilateral triangle. The measure of each angle of a triangle is 60 degrees.