Question

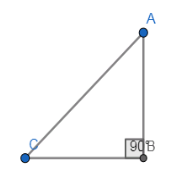
In the given figure ABC is a right triangle and right angled at B such that \[\angle BCA=2\angle BAC\].
Show that hypotenuse \[AC=2BC\]

Answer 1

Hint: In this question, let us first find the other angles with the given conditions. Then extend BC to a point D such that \[BC=BD\]. Now, from the angles we got and the equation after extending BC we can get the relation between the hypotenuse and the other side.

Complete step-by-step answer:

Now, as given in the question that \[\angle BCA=2\angle BAC\]
Let us assume \[\angle BAC\]as some variable x.
Now, by substituting this in the above equation we get,
\[\angle BCA=2x\]
As we know that the sum of the angles in a triangle is \[{{180}^{\circ }}\]we get,
\[\Rightarrow \angle BCA+\angle BAC+{{90}^{\circ }}={{180}^{\circ }}\]
Given that the triangle is right angled at B.
Now, by substituting the respective values in terms of variables in the above equation we get,
\[\Rightarrow 2x+x+{{90}^{\circ }}={{180}^{\circ }}\]
Now, on rearranging the terms and on further simplification we get,
\[\Rightarrow 3x+{{90}^{\circ }}={{180}^{\circ }}\]
Now, on subtracting \[{{90}^{\circ }}\]on both sides we get,
\[\Rightarrow 3x={{90}^{\circ }}\]
Let us now divide with 3 on the both sides then we get,
\[\begin{align}
  & \Rightarrow x=\dfrac{{{90}^{\circ }}}{3} \\
 & \therefore x={{30}^{\circ }} \\
\end{align}\]
Now, let us find the other angle by using the respective relation.
\[\begin{align}
  & \Rightarrow 2x=2\times {{30}^{\circ }} \\
 & \therefore 2x={{60}^{\circ }} \\
\end{align}\]
Hence,
\[\angle BCA={{60}^{\circ }},\angle BAC={{30}^{\circ }}\]
Now, let us extend BC to the point D and draw the diagram.

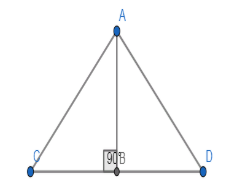
Here, \[BC=BD\]
\[\angle ABC=\angle ABD={{90}^{\circ }}\]
As given that the triangle is right angled at B.
\[AB=AB\]
As it is the common side.
Now, by using the SAS congruency we can say that,
\[\vartriangle ABC\cong \vartriangle ABD\]
Thus, we can say that,
\[\angle BAC=\angle BAD={{30}^{\circ }}\]
We can now get the angle \[\angle CAD\]
\[\Rightarrow \angle CAD=\angle BAC+\angle BAD\]
Now, on substituting the respective values we can get,
\[\begin{align}
  & \Rightarrow \angle CAD={{30}^{\circ }}+{{30}^{\circ }} \\
 & \therefore \angle CAD={{60}^{\circ }} \\
\end{align}\]
By considering the triangle ACD we can say that,
\[\Rightarrow \angle CAD+\angle BCA+\angle BDA={{180}^{\circ }}\]
Now, on substituting the corresponding values of the angles we get,
\[\begin{align}
  & \Rightarrow {{60}^{\circ }}+{{60}^{\circ }}+\angle BDA={{180}^{\circ }} \\
 & \Rightarrow \angle BDA={{180}^{\circ }}-{{120}^{\circ }} \\
 & \therefore \angle BDA={{60}^{\circ }} \\
\end{align}\]
\[\therefore \angle CAD=\angle BCA=\angle BDA={{60}^{\circ }}\]
Thus, triangle ACD is an equilateral triangle which means that all the sides are equal.
\[\Rightarrow AC=CD\]
As we already know that BC and BD are equal we can say that,
\[\begin{align}
  & \Rightarrow AC=CB+BD \\
 & \Rightarrow AC=BC+BC \\
 & \therefore AC=2BC \\
\end{align}\]

Note: It is important to extend BC to a point D where BC is equal to BD is one of the crucial steps in solving this question because if only they are equal then we can prove the congruency which in turn helps in showing that the larger triangle is an equilateral triangle.
Instead of assuming some variable to the angles in the triangle we can directly calculate them by using that their sum should be a right angle which also gives the same result. Finding these angles is important because it helps in showing that the triangle is equilateral as all of them are \[{{60}^{\circ }}\].
Two triangles that are identical in all respects are said to be congruent. Which means the corresponding sides and the corresponding are equal in those triangles. SAS congruency states that two sides and the included angle of one triangle are respectively equal to two sides and the included angle of the other triangle.