
In the given figure, ABC is a right – angled triangle such that \[\angle B = {90^ \circ }\] where, \[BC = 6\] cm and \[AB = 8\] cm respectively. Find the radius of its incircle.
A. \[10{\text{ }}cm\]
B. \[2{\text{ }}cm\]
C. \[4{\text{ }}cm\]
D. None of these

Answer
500.4k+ views
Hint: The given problem revolves around the concepts of plane geometry which includes the certain theorem of equating the tangents, sides, angles of a triangle respectively. Since, AC is break into the two parts i.e. AR and CR. As a result, to find both the values, equating the respective (adjacent) tangents of the incircle i.e. sides of the triangle respectively like \[AR = AP\], etc. substituting the value of AP i.e. \[AP + BP = AB\] from the figure assumed then using the Pythagoras’ theorem finding AC. Hence, substituting all the values from the calculations in \[AC = AR + CR\] respectively, to get the desired value.
Complete step by step answer:
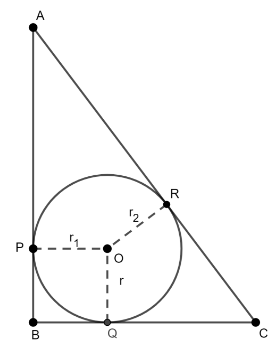
Since, we have given that \[\vartriangle ABC\] is the right-angled triangle at ‘B’ such that \[\angle B = {90^ \circ }\], Where, \[{\text{AB}} = 8cm\] and \[{\text{BC}} = 6cm\] respectively. As a result, From the given figure,
It seems that, \[r = {r_1} = {r_2}\] (same radii of incircle) is the radius of incircle of centre ‘O’ touching the sides of the respective triangle that is ‘AB’, ‘BC’ and ‘AC’ at the points ‘P’, ‘Q’ and ‘R’ respectively.Hence, from figure AP, BP, BQ, CQ, CR and AR are the tangents.As a result, by the tangent property i.e. when we extends the tangents both the respective tangents will meet at certain point, we get
\[AP = AR\] … (i)
Similarly,
\[CR = CQ\] … (ii)
And,
\[BP = BQ\] … (iii)
Since, from the figure drawn above, we get OP, OQ and OR are the respective radii of the incircle at \[OP \bot AB\], \[OQ \bot BC\] and \[OR \bot AC\] respectively where, \[\angle B = {90^ \circ }\]. Hence, from the figure it seems that \[\square PBQO\] is formed in a square geometry. Thus, we know that “All the sides of the square are always equal!”.
Hence, \[BP = BQ = r\]
As a result, from (i) we can write
\[AR = AP = AB - BP = AB - r\] … (\[\because AB = AP + BP\])
But, we have given \[AB = 8cm\]
\[AR = AP = AB - BP = 8 - r\] … (iv)
Similarly, from (ii)
\[CR = CQ = BC - BQ = BC - r\] … (\[\because BC = BQ + QC\])
But, we have given \[BC = 6cm\]
\[CR = CQ = BC - BQ = 6 - r\] … (v)
Now, applying Pythagoras Theorem as the given triangle is right-angled, we get
\[A{C^2} = A{B^2} + B{C^2}\]
Substituting the given values in the above equation, we get
\[A{C^2} = {8^2} + {6^2}\]
\[\Rightarrow A{C^2} = 64 + 36 = 100\]
Taking square roots, we get
\[AC = 100cm\] … (vi)
Now, hence from the figure it is observed that
\[AC = AR + CR\]
As a result, substituting the values from (iv), (v) and (vi) respectively in the above equation, we get
\[10 = 8 - r + 6 - r\]
\[\Rightarrow 10 = 14 - 2r\]
Hence, the required radius of the incircle is,
\[2r = 14 - 10 = 4\]
\[\therefore r = 2{\text{ }}cm\]
Hence, the correct answer is option B.
Note:One must be able to know the certain theorems in the geometry which may include side-by-side theorem, side-angle-side theorem, etc. for the accuracy in such cases.Logical thinking recommended by observing the given or any figure assumed or constructed. Since, the problem can also be find by other method by considering the area of triangle i.e. \[A = \dfrac{1}{2} \times Base \times height\] (as the triangle is right-angled) and \[A = \pi {r^2}\], equating both the equation, so as to be sure of our final answer.
Complete step by step answer:
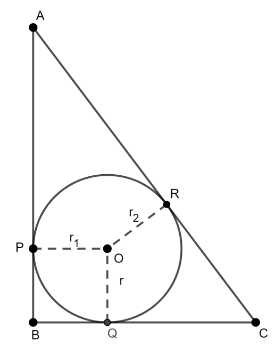
Since, we have given that \[\vartriangle ABC\] is the right-angled triangle at ‘B’ such that \[\angle B = {90^ \circ }\], Where, \[{\text{AB}} = 8cm\] and \[{\text{BC}} = 6cm\] respectively. As a result, From the given figure,

It seems that, \[r = {r_1} = {r_2}\] (same radii of incircle) is the radius of incircle of centre ‘O’ touching the sides of the respective triangle that is ‘AB’, ‘BC’ and ‘AC’ at the points ‘P’, ‘Q’ and ‘R’ respectively.Hence, from figure AP, BP, BQ, CQ, CR and AR are the tangents.As a result, by the tangent property i.e. when we extends the tangents both the respective tangents will meet at certain point, we get
\[AP = AR\] … (i)
Similarly,
\[CR = CQ\] … (ii)
And,
\[BP = BQ\] … (iii)
Since, from the figure drawn above, we get OP, OQ and OR are the respective radii of the incircle at \[OP \bot AB\], \[OQ \bot BC\] and \[OR \bot AC\] respectively where, \[\angle B = {90^ \circ }\]. Hence, from the figure it seems that \[\square PBQO\] is formed in a square geometry. Thus, we know that “All the sides of the square are always equal!”.
Hence, \[BP = BQ = r\]
As a result, from (i) we can write
\[AR = AP = AB - BP = AB - r\] … (\[\because AB = AP + BP\])
But, we have given \[AB = 8cm\]
\[AR = AP = AB - BP = 8 - r\] … (iv)
Similarly, from (ii)
\[CR = CQ = BC - BQ = BC - r\] … (\[\because BC = BQ + QC\])
But, we have given \[BC = 6cm\]
\[CR = CQ = BC - BQ = 6 - r\] … (v)
Now, applying Pythagoras Theorem as the given triangle is right-angled, we get
\[A{C^2} = A{B^2} + B{C^2}\]
Substituting the given values in the above equation, we get
\[A{C^2} = {8^2} + {6^2}\]
\[\Rightarrow A{C^2} = 64 + 36 = 100\]
Taking square roots, we get
\[AC = 100cm\] … (vi)
Now, hence from the figure it is observed that
\[AC = AR + CR\]
As a result, substituting the values from (iv), (v) and (vi) respectively in the above equation, we get
\[10 = 8 - r + 6 - r\]
\[\Rightarrow 10 = 14 - 2r\]
Hence, the required radius of the incircle is,
\[2r = 14 - 10 = 4\]
\[\therefore r = 2{\text{ }}cm\]
Hence, the correct answer is option B.
Note:One must be able to know the certain theorems in the geometry which may include side-by-side theorem, side-angle-side theorem, etc. for the accuracy in such cases.Logical thinking recommended by observing the given or any figure assumed or constructed. Since, the problem can also be find by other method by considering the area of triangle i.e. \[A = \dfrac{1}{2} \times Base \times height\] (as the triangle is right-angled) and \[A = \pi {r^2}\], equating both the equation, so as to be sure of our final answer.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




