Question

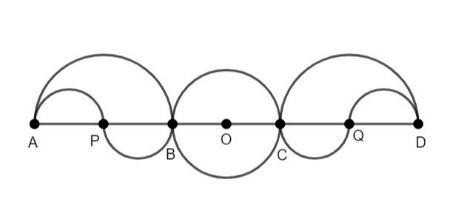
In the given figure AB = CD = 2BC = 2BP = 2CQ. In the middle, a circle with a radius of 1 cm is drawn. In the rest of the figure, all are the semicircular arcs. What is the perimeter of the whole figure?

(a). \[4\pi \]
(b). \[8\pi \]
(c). \[12\pi \]
(d). None of these

Answer 1

Hint: The perimeter of a circle of radius r is \[2\pi r\] and the perimeter of a semicircle of radius r is \[\pi r\]. Find the lengths of the radius of every semicircle and circle to find the perimeter of the whole figure.

Complete step-by-step answer:
The perimeter of a two-dimensional figure is the length of the path that surrounds the area. It is the length of the outline of the figure.
The perimeter of a circle of diameter d is also called the circumference and is given as follows:
\[C = \pi d............(1)\]
The perimeter of a semicircle is half of the circumference of the circle and is given by:
\[SC = \dfrac{{\pi d}}{2}...........(2)\]
It is given that AB = CD = 2BC = 2BP = 2CQ and the radius of the middle circle is 1 cm.
The length of BC is equal to the diameter of the middle circle, which is twice the radius of the circle.
\[BC = 2 \times 1\]
\[BC = 2cm\]
Hence, we have,
AB = CD = 2BC = 4 cm
We also have:
BP = CQ = BC = 2 cm
The circumference of the circle with diameter BC is given from equation (1) as follows:
\[{P_1} = 2\pi ............(3)\]
The perimeter of the semicircle with diameter AB is given from equation (2) as follows:
\[{P_2} = \dfrac{{4\pi }}{2}\]
\[{P_2} = 2\pi ..........(4)\]
The perimeter of the semicircle with diameter CD is given from equation (2) as follows:
\[{P_3} = \dfrac{{4\pi }}{2}\]
\[{P_3} = 2\pi ..........(5)\]
The perimeter of the semicircle with diameter BP is given from equation (2) as follows:
\[{P_4} = \dfrac{{2\pi }}{2}\]
\[{P_4} = \pi ..........(6)\]
The perimeter of the semicircle with diameter CQ is given from equation (2) as follows:
\[{P_5} = \dfrac{{2\pi }}{2}\]
\[{P_5} = \pi ..........(7)\]
The total perimeter is the sum of equations (3) to (7).
\[P = {P_1} + {P_2} + {P_3} + {P_4} + {P_5}\]
\[P = 2\pi + 2\pi + 2\pi + \pi + \pi \]
\[P = 8\pi \]
Hence, option (b) is the correct answer.

Note: You can also use symmetry to calculate the perimeter of the figure. The figure is symmetric about the middle and hence, you can calculate the perimeter of one side and multiply by two to get the answer.