Question

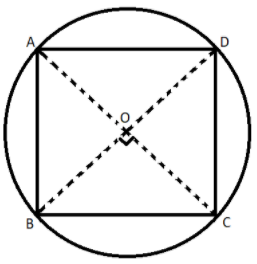
In the given figure, a square is inscribed in a circle with centre O.
Find: \[\angle OCB\]. Is BD a diameter of the circle?

Answer 1

Hint:
Here we will first draw the diagonals of the square. Then we will use the property of the diagonals of the square to get the value of the angle BOC. Then we will use the property of the sum of all the interior angles of a triangle to get the value of the angle OCB.

Complete Step by Step Solution:
It is given that ABCD is a square which is inscribed in a circle with centre O.
AC and BD are the diagonal of the square ABCD. We know the property of the square that diagonals of the square intersect each other at a right angle i.e. at \[90^\circ \].
Therefore, the angle BOC is \[\angle BOC = 90^\circ \].

We know that the sum of all the interior angles of a triangle is equal to \[180^\circ \]. So, by using this condition we will write the sum of all the angle of the triangle BOC, we get
\[\angle OBC + \angle OCB + \angle BOC = 180^\circ \]
Also, the angle OBC is equal to the angle OCB i.e. \[\angle OBC = \angle OCB\]. Therefore, we get
\[\angle OCB + \angle OCB + 90^\circ = 180^\circ \]
Subtracting \[90^\circ \] from both sides, we get
\[ \Rightarrow 2\angle OCB = 180^\circ - 90^\circ = 90^\circ \]
Dividing both sides by 2, we get
\[ \Rightarrow \angle OCB = \dfrac{{90^\circ }}{2} = 45^\circ \]
Hence the value of the angle \[\angle OCB\] is equal to \[45^\circ \].
We can see that the diagonal BD of the square is equal to the diameter of the circle with the center O.

Therefore, BD is the diameter of the circle.

Note:
Diagonals of the square is also the angle bisector of the angle of the end vertices of that diagonal of the square. In geometry, bisection is the division of something into two equal parts. There are two main types of bisectors and they are line segment bisector and angle bisector. A line segment bisector is a line or line segment that divides the line into two equal parts or which passes through the midpoint of the line segment. An angle bisector is the line or line segment that divides an angle into two equal parts.