Question

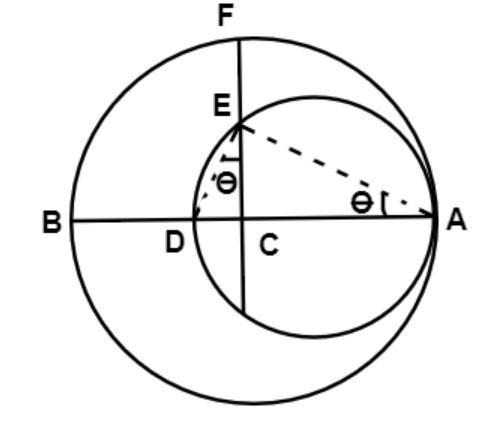
In the given figure a crescent is formed by two circles which touch at A. C is the center of the larger circle. The width of the crescent at BD is 9 cm and at EF it is 5 cm. Find the radii of two circles.

Answer 1

Hint – In this particular type of question use the concept of similar triangle when one side is common to both the triangle $i.e.\dfrac{{AC}}{{CE}} = \dfrac{{CE}}{{CD}}$, and the width of the crescent is nothing but the length of BD, so use this concept to reach the solution of the question.

Complete step by step solution:
Given data:
Width of the crescent BD is 9cm.
Therefore, BD = 9 cm.
Width of crescent EF is 5cm.
Therefore, EF = 5cm.
And from figure, $\angle CAE = \angle CED = \theta $
Now it is given that C is the center of the big circle.
So AB is the diameter of the big circle and AD is the diameter of the smaller circle.
Therefore, from figure,
BD = AB – AD
Now let the diameter of the big circle be D cm and the diameter of the smaller circle be d cm.
Therefore, AB = D cm, and AD = d cm.
Therefore, BD = 9 = D – d.
Now as we know that the diameter is twice of the radius so,
D = 2R and d = 2r, where R and r is the radius of a bigger and smaller circle respectively.
Therefore, 2R – 2r = 9
Therefore, R – r = 4.5cm.................. (1)
And AC = CB = CF = R cm......................... (2)
Now from figure CF is the radius of the bigger circle.
Therefore, CF = R
Now again from figure, EF = CF – CE
Therefore, 5 = R – CE
Therefore, CE = R – 5..................... (3)
Now from figure CD = CB – BD
Therefore, CD = R – 9.............. (4)
Now in triangle AEC and in triangle DEC
$\angle CAE = \angle CED = \theta $
CE = CE (common)
$\angle ACE = \angle DCE = {90^o}$
So by ASA congruence triangle AEC and triangle DEC are similar.
So by property of similar triangle we have,
$ \Rightarrow \dfrac{{AC}}{{CE}} = \dfrac{{CE}}{{CD}}$
Now substitute the values of AC, CE and CD from equation (2), (3) and (4) we have,
$ \Rightarrow \dfrac{R}{{R - 5}} = \dfrac{{R - 5}}{{R - 9}}$
Now simplify this we have,
$ \Rightarrow R\left( {R - 9} \right) = \left( {R - 5} \right)\left( {R - 5} \right)$
$ \Rightarrow {R^2} - 9R = {R^2} + 25 - 10R$
$ \Rightarrow 10R - 9R = 25$
$ \Rightarrow R = 25$
Now from equation (1) we have,
$ \Rightarrow 25 - r = 4.5$
$ \Rightarrow r = 25 - 4.5 = 20.5$ Cm.
So the radius of the bigger circle is 25cm and the smaller circle is 20.5cm.
So this is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that always recall that the diameter of the circle is double the radius, so first find out the length of BD in terms of radius of the circles and then find the length of CD and CE and above, then apply similar triangle property as above and simplify we will get the required radius of the circles.