Question

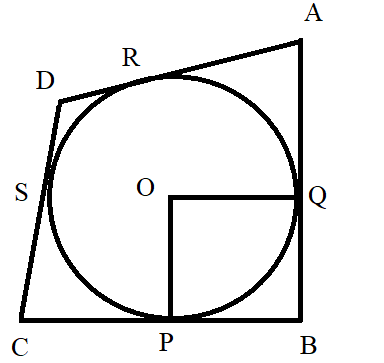
In the given figure, a circle with centre O is inscribed in a quadrilateral ABCD such that it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB$ = 29cm$, AD$ = 23\,cm$, $\angle B = {90^\circ }$ and DS$ = 5\,cm$, then the radius of the circle (in cm) is:

(a) $11$
(b) $18$
(c) $6$
(d) $15$

Answer 1

Hint:In the given question, we are provided with a figure consisting of a quadrilateral in which a circle of unknown radius is inscribed. The sides AB, BC, CD, and DA of the quadrilateral ABCD touches the circle at points P, Q, R and S. We need to have some basic knowledge of the properties of tangents to the circle in order to solve such questions.

Complete step by step answer:
So, the four sides of the quadrilateral are tangents for the circle and we are given measures of some segments with the help of which we have to find the radius of the circle.
So, we are given that AB$ = 29cm$, AD$ = 23\,cm$, $\angle B = {90^\circ }$ and DS$ = 5\,cm$.
Now, we know that the length of tangents from an external point is equal. So, we can apply the property in the question to find the radius of the circle.
So, we know that DS$ = 5\,cm$. DS and DR are the tangents to the circle from the same external point D. Hence, DR$ = $DS$ = 5\,cm$.
Now, AD$ = 23\,cm$.
$ \Rightarrow $$AR + DR = 23\,cm$
Substituting the length of DR, we get,
$ \Rightarrow $$AR + 5\,cm = 23\,cm$
$ \Rightarrow $$AR = 23\,cm - 5\,cm$
Simplifying the calculations, we get,
$ \Rightarrow $$AR = 18\,cm$
So, the length of AR is $18\,cm$.
Now, AR and AQ are the tangents to the circle from the same external point A. Hence, $AR = AQ = 18\,cm$.
Also, AB$ = 29cm$.
$ \Rightarrow $$AQ + QB = 29\,cm$
$ \Rightarrow $$18\,cm + QB = 29\,cm$
Simplifying the calculations, we get,
$ \Rightarrow $$QB = 29\,cm - 18\,cm$
$ \Rightarrow $$QB = 11\,cm$
Now, we are given that $\angle B = {90^\circ }$. Also, we know that tangent is always perpendicular to the radius of the circle. Hence, all the angles in the “quadrilateral OPQB” are right angles. Also, the length of BQ and PQ is the same as they are tangents to the circle from the same external point. So, we can conclude that the quadrilateral OQBP is a square. Hence, the length of OP is equal to the length of BQ.
Thus, $OP = 11\,cm$
Therefore, the radius of the circle is $11\,cm$.

Note: Such questions require a strong grip over basic concepts of circles and tangents. One should be confident in such geometrical problems so as to attempt and solve the given question. We can also verify the answer by doing the question backwards.