Question

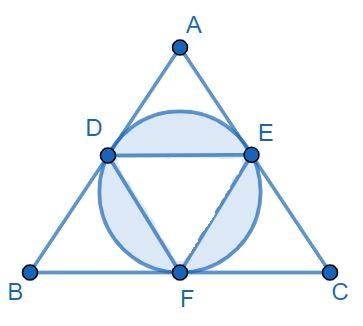
In the given diagram, ABC is an equilateral triangle whose side is $2\sqrt{3}cm$. A circle is drawn which passes through the midpoints D,E and F of its sides. The area of the shaded region is:

a) $\dfrac{1}{4}\left( 4\pi -3\sqrt{3} \right)c{{m}^{2}}$
b) $\dfrac{1}{4}\left( 2\pi -\sqrt{3} \right)c{{m}^{2}}$
c) $\dfrac{1}{4}\left( \pi -3\sqrt{3} \right)c{{m}^{2}}$
d) $\dfrac{1}{4}\left( 3\pi -\sqrt{3} \right)c{{m}^{2}}$

Answer 1

Hint: We will use the proportionality theorem to show that $\Delta DEF$ is an equilateral triangle. Area of the equilateral triangle is equal to $\dfrac{\sqrt{3}}{4}{{a}^{2}}$, where a is the side of an equilateral triangle. Also, area of circle is given by formula $\pi {{r}^{2}}$ here the given circle is circumscribe in $\Delta ABC$, so radius of circle is equal to $\dfrac{\Delta }{S}$ here $\Delta $ is area of equilateral triangle and ‘S’ is the half of the perimeter of $\Delta ABC$. Shaded region is given by area of circle – area of $\Delta ABC$.

Complete step-by-step answer:
It is given in the question that ABC is an equilateral triangle whose side is $2\sqrt{3}cm$. A circle is drawn which passes through the mid-points D,E and F of its sides, then we have to find out the area of the shaded region.
The triangle proportionality theorem states that if a line is parallel to one side of a triangle and it intersects the other two sides, then it divides those sides proportionally.

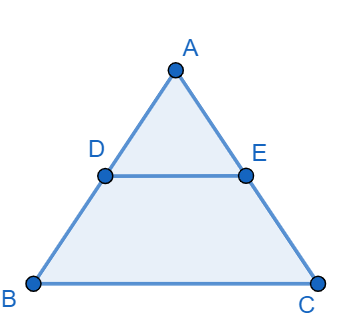
Here DE is half of BC.
It is noted that the smaller triangle is also equilateral because all the sides of the triangle DEF are exactly half of the sides of triangle ABC.
On the basis of proportionality theorem, $BE=\dfrac{BC}{2}$, $EF=\dfrac{AB}{2}$ and $DE=\dfrac{AC}{2}$.
In the given question figure,

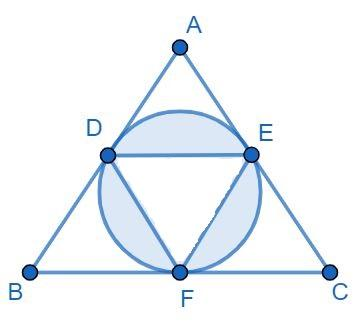
Circle is inscribed in the equilateral triangle ABC, the radius of circle is given by $\dfrac{\Delta }{S}$ because the circle is inscribed in the equilateral $\Delta ABC$, here $\Delta $ is area of equilateral triangle and ‘S’ is the half of the perimeter of $\Delta ABC$.
S is calculated as $\dfrac{\text{Sum of perimeter}}{2}$
= $\dfrac{2\sqrt{3}+2\sqrt{3}+2\sqrt{3}}{2}=3\sqrt{3}$.
Therefore radius of circle $=\dfrac{\dfrac{\sqrt{3}}{4}{{\left( 2\sqrt{3} \right)}^{2}}}{3\sqrt{3}}=\dfrac{\dfrac{\sqrt{3}}{4}\times 4\times 3}{3\sqrt{3}}$, which can be calculated as
= $\dfrac{3\sqrt{3}}{3\sqrt{3}}=1$.
Hence area of circle = $\pi {{r}^{2}}=3.14\times {{1}^{2}}=3.14c{{m}^{2}}=\pi c{{m}^{2}}$.
Now area of smaller equilateral triangle DEF with side $a=\dfrac{2\sqrt{3}}{2}cm$ is $=\dfrac{\sqrt{3}}{4}{{\left( \dfrac{2\sqrt{3}}{2} \right)}^{2}}=\dfrac{3\sqrt{3}}{4}c{{m}^{2}}$.
Therefore the area of required region is given as $=area\text{ }of\text{ }circle\text{ }-\text{ }area\text{ }of\text{ }\Delta DEF$, putting the values we get,
$=\left( \pi -\dfrac{3\sqrt{3}}{4} \right)c{{m}^{2}}$ which can be written as
$=\dfrac{1}{4}\left( 4\pi -3\sqrt{3} \right)c{{m}^{2}}$.
Thus option a) is the correct answer.

Note: Usually students do miss-calculate in finding the radius of the circle. Many students do not know that we can calculate the radius of an inscribed circle using formula \[r=\dfrac{\Delta }{S}\]. Also, some students take S as a perimeter whereas actually it is half of the perimeter.