Question

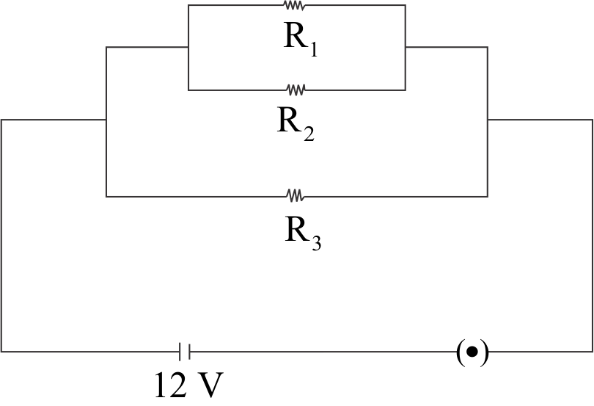
In the given circuit diagram ${R_1} = 5\Omega $, ${R_2} = 10\Omega $ and ${R_3} = 20\Omega $. Calculate the total resistance of the circuit.

Answer 1

Hint: All the resistances in the given diagram are connected in parallel to each other. So we need to use the formula for parallel connections to calculate the effective resistance.
Formula used
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ where $R$ is the effective resistance, ${R_1}$ and ${R_2}$ are two resistances which are connected in parallel.

Complete step by step answer
As we see in the given diagram, resistances ${R_1}$ and ${R_2}$ are connected parallel to one another.
Parallel connections mean that the branches have the same potential difference but different current. In this case it means that both the resistances are joined from both the sides. Whereas series connection means that only one hand of the resistances are connected to each other. In series connections, the potential difference between the resistances are different but the current flowing through them remains constant.
So let $R'$ be their equivalent resistance
Therefore,
 $\begin{gathered}
  \dfrac{1}{{R'}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \\
   \Rightarrow R' = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \\
\end{gathered} $
Substituting the values ${R_1} = 5\Omega $ and ${R_2} = 10\Omega $ in the above equation, we get,
$\begin{gathered}
  R' = \dfrac{{5 \times 10}}{{5 + 10}} \\
   \Rightarrow R' = \dfrac{{50}}{{15}} = \dfrac{{10}}{3} \\
\end{gathered} $
Now, this equivalent resistance is also in parallel connection with ${R_3}$
So, the total resistance $R$ in the circuit become,
$\begin{gathered}
  \dfrac{1}{R} = \dfrac{1}{{R'}} + \dfrac{1}{{{R_3}}} \\
   \Rightarrow R = \dfrac{{R'{R_3}}}{{R' + {R_3}}} \\
\end{gathered} $
Substituting values in the above equation we get,
$R = \dfrac{{\dfrac{{10}}{3} \times 20}}{{\dfrac{{10}}{3} + 20}} = \dfrac{{20}}{7}\Omega $

Hence, the total resistance in the circuit is $\dfrac{{20}}{7}\Omega $.

Note: In this question we are only being asked to calculate the effective resistance of the circuit, but if we were also asked to calculate the current flowing through the circuit, we can use the ohm’s law to determine that. Ohm’s law states that the current flowing through a circuit between two points is directly proportional to the potential difference between the two points at constant temperature and other physical conditions. It is given by the relation $V = iR$ where $V$ is the p.d, $i$ is the current and $R$ is the effective resistance.