Question

In the following figure, which of the following is the value of $\csc \theta $?

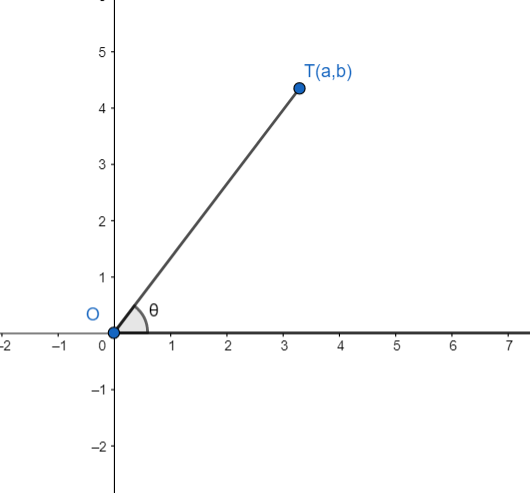
[a] $\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
[b] $\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
[c] $\dfrac{b}{a}$
[d] $\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}$
[e] $\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{b}$

Answer 1

Hint: Use the fact that $\tan \theta $ is the slope of the line OT. Hence find the value of $\tan \theta $. Using the Pythagorean identity ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta $, find the value of $\sec \theta $ and hence find the value of $\cos \theta $.
Using the fact that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$, find the value of $\sin \theta $ and hence find the value of $\csc \theta $. Hence find which of the options is correct.

Complete step-by-step answer:

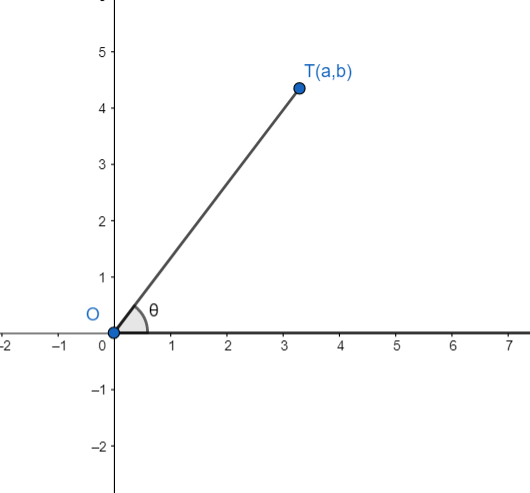
We know that the tangent of the angle made by a line with the positive direction of x-axis is the slope of the line.
Hence, we have
Slope of the line OT $=\tan \theta $
Now, we know that the slope of the line joining the poits $A\left( {{x}_{1}},{{y}_{1}} \right)$and $B\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Hence, we have
Slope of the line OT $=\dfrac{b-0}{a-0}=\dfrac{b}{a}$
Hence, we have $\tan \theta =\dfrac{b}{a}$
We know that ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta $
Hence, we have
${{\sec }^{2}}\theta =1+\dfrac{{{b}^{2}}}{{{a}^{2}}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}}$
Hence, we have
$\sec \theta =\pm \dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}$
Since $\theta $ lies in the first quadrant, we have $\sec \theta >0$
Hence, we have
$\sec \theta =\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}$
We know that $\cos \theta =\dfrac{1}{\sec \theta }$
Substituting the value of $\sec \theta $, we get
$\cos \theta =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
Now, we know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$
Substituting the values of $\tan \theta $ and $\cos \theta $, we get
$\dfrac{b}{a}=\dfrac{\sin \theta }{\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}}$
Multiplying both sides by $\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$, we get
$\sin \theta =\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
We know that $\csc \theta =\dfrac{1}{\sin \theta }$
Substituting the value of $\sin \theta $, we get
$\csc \theta =\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{b}$
Hence option [e] is correct.

Note: Alternative solution:
Draw perpendicular TA and TB on the x-axis and the y-axis, respectively.

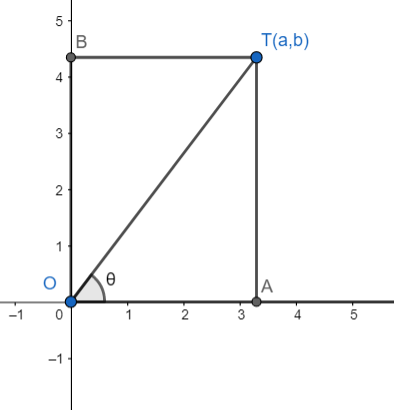
Hence, we have OA = a and OB = b.
Now, in triangle OAT, by Pythagoras theorem, we have
$O{{T}^{2}}={{a}^{2}}+{{b}^{2}}\Rightarrow OT=\sqrt{{{a}^{2}}+{{b}^{2}}}$
We know that cosecant of an angle is the ratio of the hypotenuse to the opposite side.
Hence, we have
$\csc \theta =\dfrac{OT}{AT}=\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{b}$, which is the same as obtained above
Hence option [e] is correct.