Question

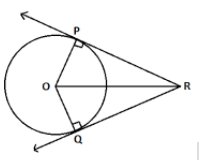
In the following figure, two tangents RQ and RP are drawn from an external point R to the circle with center O, If$\angle PRQ = 120^\circ $ , then prove that $OR = PR + RQ$.
               

Answer 1

Hint: To solve this problem, first we will obtain $\angle PRO = QRO$ using side-side-side congruent theorem of triangle. Then we will obtain $\angle PRO$. Then from triangle POR we will prove $OR = PR + RQ$

Complete step-by-step answer:
According to the question,
Two tangents RQ and RP are drawn from an external point R to the circle with center O i.e.
RQ = RP ( Tangents are drawn from the same point to the circle are equal in length)
$\angle PRQ = 120^\circ $
In $\vartriangle POR$ and $\vartriangle QOR$,
$OP = OQ$ (As the radii of the same circle)
$RP = RQ$ (From given data)
OR is the common side.
By the side-side-side congruence theorem of the triangle, both the above triangles are congruent.
Hence, $\angle PRO = \angle QRO$ (As corresponding parts of congruent triangles are equal.)
Now we know that, $\angle PRQ = 120^\circ $
We can write $\angle PRQ$ as $\angle PRO + QRO$
i.e. $\angle PRO + QRO = 120^\circ $
As we know, $\angle PRO = \angle QRO$, then the above equation becomes,
$\angle PRO + \angle PRO = 120^\circ $
$ \Rightarrow 2\angle PRO = 120^\circ $
Dividing two on the both of the sides of the equation we get,
$\dfrac{{2\angle PRO}}{2} = \dfrac{{120^\circ }}{2}$
$ \Rightarrow \angle PRO = 60^\circ $
In right angled $\vartriangle POR$,
$\cos 60^\circ = \dfrac{{PR}}{{OR}}$
Putting value of $\cos 60^\circ $ in above equation,
$\dfrac{{PR}}{{OR}} = \dfrac{1}{2}$
By doing cross multiplication we get,
$OR = 2PR$
We can write the above equation as,
$OR = PR + PR$
As $RP = RQ$, putting RQ in place of one PR we get,
$OR = PR + RQ$
Hence, it is proved that $OR = PR + RQ$

Note: Tangents are drawn from the same point to the circle are equal in length.
You should remember all the formulas and rules related to tangents of the circle.
The side-side-side theorem of triangle states that if three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are congruent.
You should remember all congruence theorems of triangles.
Corresponding parts of congruent triangles are equal.