Question

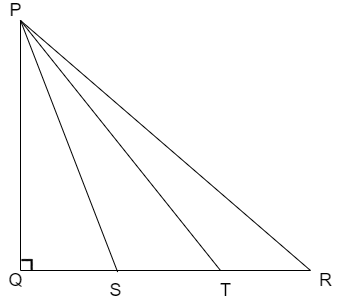
In the following figure, S and T trisect the side QR of a right angle triangle \[\Delta PQR\] then prove that \[8P{{T}^{2}}=3P{{R}^{2}}+5P{{S}^{2}}\]

Answer 1

Hint: We solve this problem by using the Pythagoras theorem. The Pythagoras theorem states that the square of the hypotenuse is equal to the sum of squares of the other two sides that is for the triangle shown below

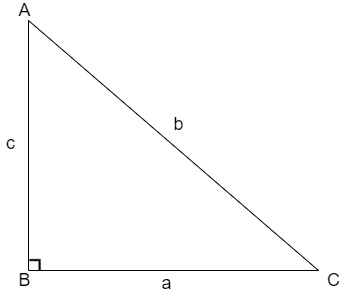
The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
We use this theorem for all the possible triangles in the given figure to prove the required result using the condition that S and T trisect the side QR which means \[QS=ST=TR=\dfrac{QR}{3}\]
Complete step by step solution:
We are given that S and T trisect the side QR
By converting the above statement into a mathematical equation we get
\[\Rightarrow QS=ST=TR=\dfrac{QR}{3}\]
We know that the Pythagoras theorem that the square of the hypotenuse is equal to the sum of squares of the other two sides that is for the triangle shown below

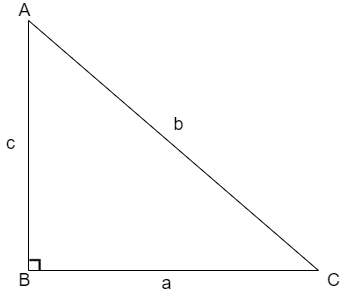
The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
Now, let us consider the triangle \[\Delta PQR\]
By applying the Pythagoras theorem to \[\Delta PQR\] we get
\[\Rightarrow P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}\]
Now, let us consider the triangle \[\Delta PQS\]
By applying the Pythagoras theorem to \[\Delta PQS\] we get
\[\Rightarrow P{{S}^{2}}=P{{Q}^{2}}+Q{{S}^{2}}\]
Now, let us consider the triangle \[\Delta PQT\]
By applying the Pythagoras theorem to \[\Delta PQT\] we get
\[\Rightarrow P{{T}^{2}}=P{{Q}^{2}}+Q{{T}^{2}}\]
We are asked to prove that
\[8P{{T}^{2}}=3P{{R}^{2}}+5P{{S}^{2}}\]
Let us take the RHS and try to prove LHS
Let us assume that the LHS as
\[\Rightarrow LHS=3P{{R}^{2}}+5P{{S}^{2}}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow LHS=3\left( P{{Q}^{2}}+Q{{R}^{2}} \right)+5\left( P{{Q}^{2}}+Q{{S}^{2}} \right) \\
 & \Rightarrow LHS=8P{{Q}^{2}}+3Q{{R}^{2}}+5Q{{S}^{2}}........equation(i) \\
\end{align}\]
Now, let us find the values of QR and QS in terms of QT
We are given that
\[\Rightarrow QS=ST=TR=\dfrac{QR}{3}\]
From the figure we can take the value of QT as
\[\Rightarrow QT=QS+ST\]
By substituting the values of QS and ST in terms of QR in above equation we get
\[\begin{align}
  & \Rightarrow QT=\dfrac{QR}{3}+\dfrac{QR}{3} \\
 & \Rightarrow QT=\dfrac{2}{3}QR \\
 & \Rightarrow QR=\dfrac{3}{2}QT......equation(ii) \\
\end{align}\]
Now, similarly from the figure we can write the value of QS as
\[\begin{align}
  & \Rightarrow QS=QR-SR \\
 & \Rightarrow QS=QR-\left( ST+TR \right) \\
\end{align}\]
By substituting the values of ST and TR in terms of QR in above equation we get
\[\begin{align}
  & \Rightarrow QS=QR-\left( \dfrac{QR}{3}+\dfrac{QR}{3} \right) \\
 & \Rightarrow QS=QR-\dfrac{2}{3}QR \\
 & \Rightarrow QS=\dfrac{1}{3}QR \\
\end{align}\]
Now, by substituting the value of QR from equation (ii) in above equation we get
\[\begin{align}
  & \Rightarrow QS=\dfrac{1}{3}\left( \dfrac{3}{2}QT \right) \\
 & \Rightarrow QS=\dfrac{1}{2}QT.......equation(iii) \\
\end{align}\]
Now, by substituting the equation (ii) and equation (iii) in equation (i) we get
\[\begin{align}
  & \Rightarrow RHS=8P{{Q}^{2}}+3{{\left( \dfrac{3QT}{2} \right)}^{2}}+5{{\left( \dfrac{QT}{2} \right)}^{2}} \\
 & \Rightarrow RHS=8P{{Q}^{2}}+Q{{T}^{2}}\left( \dfrac{27}{4}+\dfrac{5}{4} \right) \\
 & \Rightarrow RHS=8\left( P{{Q}^{2}}+Q{{T}^{2}} \right) \\
\end{align}\]
We know that from the Pythagoras theorem to \[\Delta PQT\] we get
\[\Rightarrow P{{T}^{2}}=P{{Q}^{2}}+Q{{T}^{2}}\]
By substituting this value in above equation we get
\[\begin{align}
  & \Rightarrow RHS=8P{{T}^{2}} \\
 & \Rightarrow RHS=LHS \\
\end{align}\]
Therefore, we can conclude that
\[\therefore 8P{{T}^{2}}=3P{{R}^{2}}+5P{{S}^{2}}\]
Hence the required result has been proved.

Note: This problem can be solved in another method.
From the Pythagoras theorem to all possible triangles we have the equations
\[\Rightarrow P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}.......equation(iv)\]
\[\Rightarrow P{{S}^{2}}=P{{Q}^{2}}+Q{{S}^{2}}......equation(v)\]
\[\Rightarrow P{{T}^{2}}=P{{Q}^{2}}+Q{{T}^{2}}......equation(vi)\]
By subtracting equation (vi) from equation (iv) we get
\[\Rightarrow P{{R}^{2}}-P{{T}^{2}}=Q{{R}^{2}}-Q{{T}^{2}}\]
By substituting the value of QT from equation (ii) we get
\[\begin{align}
  & \Rightarrow P{{R}^{2}}-P{{T}^{2}}= Q{{R}^{2}}- {{\left( \dfrac{2QR}{3} \right)}^{2}} \\
 & \Rightarrow P{{R}^{2}}-P{{T}^{2}}=\dfrac{5Q{{R}^{2}}}{9}.......equation(vii) \\
\end{align}\]
Now, by subtracting equation (v) from equation (vI) we get
\[\Rightarrow P{{T}^{2}}-P{{S}^{2}}=Q{{T}^{2}}-Q{{S}^{2}}\]
By substituting the value of QT from equation (ii) and value of QS from equation (iii) we get
\[\begin{align}
  & \Rightarrow P{{T}^{2}}-P{{S}^{2}}={{\left( \dfrac{2QR}{3} \right)}^{2}}-{{\left( \dfrac{QR}{3} \right)}^{2}} \\
 & \Rightarrow P{{T}^{2}}-P{{S}^{2}}=\dfrac{3Q{{R}^{2}}}{9}...........equation(viii) \\
\end{align}\]
Now, let us multiply 3 to equation (vii) and 5to equation (viii), then by subtracting them together we get
\[\begin{align}
  & \Rightarrow 3\left( P{{R}^{2}}-P{{T}^{2}} \right)-5\left( P{{T}^{2}}-P{{S}^{2}} \right)=\dfrac{15Q{{R}^{2}}}{9}-\dfrac{15Q{{R}^{2}}}{9} \\
 & \Rightarrow 8P{{T}^{2}}=3P{{R}^{2}}+5P{{S}^{2}} \\
\end{align}\]
Hence the required result has been proved.