Question

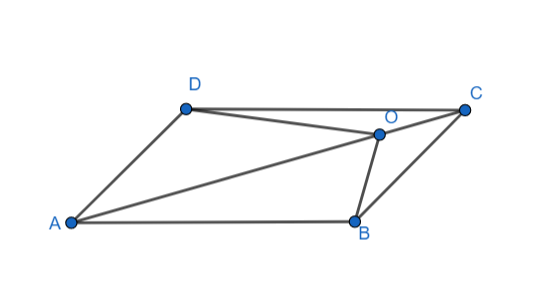
In the following figure O is a point on the diagonal AC of parallelogram ABCD. Prove that $ar\left( \Delta AOB \right)=ar\left( \Delta AOD \right)$

Answer 1

Hint: Join BD and mark E as the point of intersection of BD with AC. Use the fact that the diagonals of a parallelogram bisect each other to prove that E is the midpoint of BD. Now, use the fact that the median of a triangle divides the triangle into two triangles of equal area. Hence prove that the areas of the triangles ADE and ABE are equal. Similarly, prove that the areas of the triangle BOE and DOE are equal and hence prove that the areas of the triangles AOD and AOB are equal.

Complete step-by-step answer:

Given: ABCD is a parallelogram. O is a point on the diagonal AC.
To prove: Triangles AOD and AOB are equal in area, i.e. $ar\left( \Delta AOB \right)=ar\left( \Delta AOD \right)$
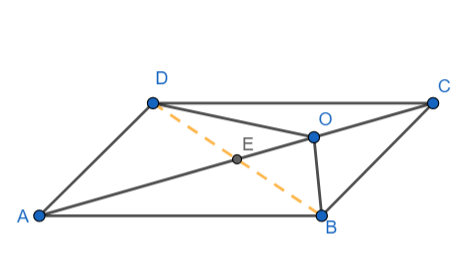
Construction: Join BD and let it intersect AC at E
Proof:
We know that the diagonals of a parallelogram bisect each other. Hence, we have AC bisects BD
Hence, E is the midpoint of BD.
Now, in triangle ABD, we have E as the midpoint of BD.
Hence, $ar\left( \Delta AED \right)=ar\left( \Delta AEB \right)\text{ }\left( i \right)$(Because the median of a triangle divides the triangle into two triangles of equal area.)
In triangle BOD, we have E as the midpoint of BD.
Hence we have $ar\left( \Delta BOE \right)=ar\left( \Delta DOE \right)\text{ }\left( ii \right)$(Because the median of a triangle divides the triangle into two triangles of equal area.)
Adding equation (i) and equation (ii), we get
$ar\left( \Delta AED \right)+ar\left( \Delta DOE \right)=ar\left( \Delta BOE \right)+ar\left( \Delta AEB \right)$
From the above diagram, we have
$ar\left( \Delta AED \right)+ar\left( \Delta DOE \right)=ar\left( \Delta AOD \right)$ and $ar\left( \Delta BOE \right)+ar\left( \Delta AEB \right)=ar\left( \Delta AOB \right)$
Hence, we have
$ar\left( \Delta AOD \right)=ar\left( \Delta AOB \right)$
Hence proved.

Note: Alternative solution:

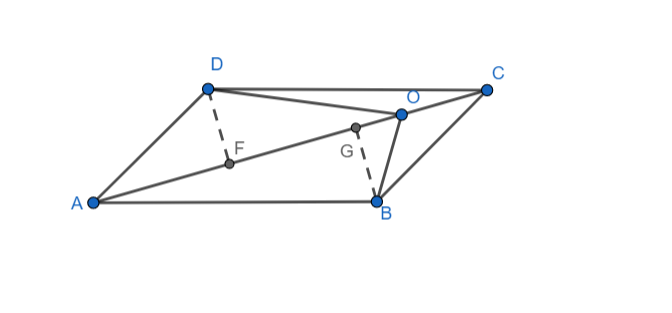
Draw perpendiculars DF and BG on diagonal AC.
Now, we know that the diagonal of a parallelogram divides the parallelogram into two congruent triangles.
Hence, we have
$ar\left( \Delta ACD \right)=ar\left( \Delta ABD \right)$
We know that the area of a triangle is half the product of base and height.
Hence, we have
$ar\left( \Delta ACD \right)=\dfrac{1}{2}DF\times AC$ and $ar\left( \Delta ACB \right)=\dfrac{1}{2}BG\times AC$
Hence, we have
$\begin{align}
  & \dfrac{1}{2}DF\times AC=\dfrac{1}{2}AC\times BG \\
 & \Rightarrow DF=BG \\
\end{align}$
Now, we have
$ar\left( \Delta AOD \right)=\dfrac{1}{2}DF\times AO$ and $ar\left( \Delta AOB \right)=\dfrac{1}{2}BG\times AO$
Hence, we have
$\dfrac{ar\left( \Delta AOD \right)}{ar\left( \Delta AOB \right)}=\dfrac{DF}{BG}=\dfrac{DF}{DF}=1$
Multiplying both sides by $ar\left( \Delta AOB \right)$, we get
$ar\left( \Delta AOD \right)=ar\left( \Delta AOB \right)$