Question

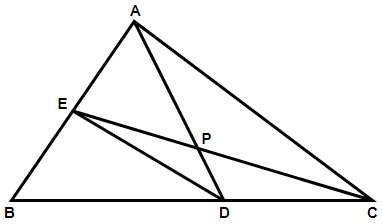
In the following figure, AE = EB, BD = 2DC. What is the ratio of the areas of PED and ABC?

Answer 1

Hint: Assume the areas of the triangles APE, BED and PDC as p, q and r respectively and join the points P and B. Use the theorem that ‘the ratio of area of triangles with same height is equal to the ratio of their bases’ to form two linear relations between p and r. Solve the two equations for the value of p in terms of q and area of PED and substitute it in any one of the equations. Use the relation 3q = Area (ABC) to get the ratio of areas of required triangles.

Complete step-by-step solution:
Here we have been provided with the figure shown below in which AE = EB and BD = 2DC. We are asked to find the ratio of the areas of triangles PED and ABC. Let us use some properties of triangles having the same height but different base length to get the answer.

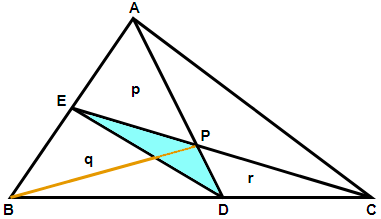
Now, in the above figure we have assumed the area of the triangles APE, BDE and PDC as p, q and r respectively. Also, we have joined the points P and B. We know that we can write the area of the triangle ABC as Area (ABC) = $\dfrac{1}{2}\times \text{AB}\times \text{BC}\times \sin B$, similarly the area of the triangle BED can be given as q = $\dfrac{1}{2}\times \text{BE}\times \text{BD}\times \sin B$. So using the given relations AE = EB and BD = 2BC we can write $\text{BE}=\dfrac{\text{AB}}{2}$ and $\text{BD}=\dfrac{2\text{BC}}{3}$ respectively, so we get,
\[\begin{align}
  & \Rightarrow q=\dfrac{1}{2}\times \dfrac{\text{AB}}{2}\times \dfrac{2\text{BC}}{3}\times \sin B \\
 & \Rightarrow q=\dfrac{1}{3}\times \left( \dfrac{1}{2}\times \text{AB}\times \text{BC}\times \sin B \right) \\
\end{align}\]
$\Rightarrow q=\dfrac{1}{3}\times $ Area (ABC) …….. (i)
Now, in triangles PDC and PBD we have their heights equal and the base DC and BD is in the ratio 1:2 so their areas will also be in the ratio 1:2. Therefore we have,
$\Rightarrow $ 2Area (PDC) = Area (PBD)
$\Rightarrow $ 2r = Area (PBD) ………. (1)
Similarly, in triangles APE and PBE we have their heights equal and the base AE and EB is in the ratio 1:1 so their areas will also be in the ratio 1:1. Therefore we have,
$\Rightarrow $ Area (APE) = Area (PBE)
$\Rightarrow $ p = Area (PBE) ……… (2)
Adding equations (1) and (2) we get,
$\Rightarrow $ p + 2r = Area (PBD) + Area (PBE)
Here, Area (PBD) + Area (PBE) equals the total area of the quadrilateral PEBD which in turn is equal to the combination of areas of the triangles PED and BED, so we can write,
$\Rightarrow $ p + 2r = q + Area (PED) ……… (3)
In triangles ADE and BDE we have their bases AE and EB in the ratio 1:1, so we get,
$\Rightarrow $ Area (ADE) = Area (BDE)
$\Rightarrow $ p + Area (PED) = q ……… (4)
Similarly, in triangles CDE and BDE we have their bases CD and BD in the ratio 1:2, so we get,
$\Rightarrow $ 2Area (CDE) = Area (BD)
$\Rightarrow $ 2r + 2Area (PED) = q ……… (5)
From equations (4) and (5) we can write,
$\Rightarrow $ p + Area (PED) = 2r + 2Area (PED)
$\Rightarrow $ p – 2r = Area (PED) ……… (6)
Now, we have two linear relations between p and r (equations (3) and (6)), so adding these two equations we get,
$\Rightarrow $ 2p = q + 2Area (PED)
$\Rightarrow p=\dfrac{q}{2}+$ Area (PED)
Substituting the above obtained value of p in equation (4) we get,
\[\Rightarrow \dfrac{q}{2}+\] Area (PED) + Area (PED) = $q$
$\Rightarrow $ 2Area (PED) = \[\left( q-\dfrac{q}{2} \right)\]
$\Rightarrow $ Area (PED) = \[\dfrac{q}{4}\]
Using equation (i) and substituting the value of q in terms of area of the triangle ABC we get,
$\Rightarrow $ Area (PED) = \[\dfrac{1}{4}\times \dfrac{1}{3}\times \] Area (ABC)
$\Rightarrow $ Area (PED) = $\dfrac{1}{12}\times $ Area (ABC)
$\therefore \dfrac{\text{Area }\left( \text{PED} \right)}{\text{Area }\left( \text{ABC} \right)}=\dfrac{1}{12}$
Hence, the ratio of the areas of the triangles PED and ABC is 1:12.

Note: Note that in case the lengths of the bases of the triangles are same and their heights are different then the ratio of areas of the triangles is the ratio of their heights. In case both are different for two triangles then the ratio of areas is the ratio of product of their base and height. Also, remember the important formula of the area of a triangle given by ‘half of the product of two sides and the sine of the included angle between them’.