Question

In the following figure, ABCD is a trapezium with AB parallel to DC. If AB = 9cm, BC = 18 cm, CF = 13.5 cm, AP = 6cm and BE = 15cm. Calculate PE.

(a) PE = 5.8 cm
(b) PE = 4.8 cm
(c) PE = 2.8 cm
(d) PE = 3.8 cm

Answer 1

Hint: For solving this problem, we have to prove that triangle APD and BPE are similar. Now, by using the property of similar triangles, we can equate the ratio of sides to obtain the desired length.

Complete Step-by-Step solution:
According to this problem, we are given a trapezium ABCD with AB parallel to DC. We are given some other known length in the figure. Now, on reconstructing the figure we obtain:

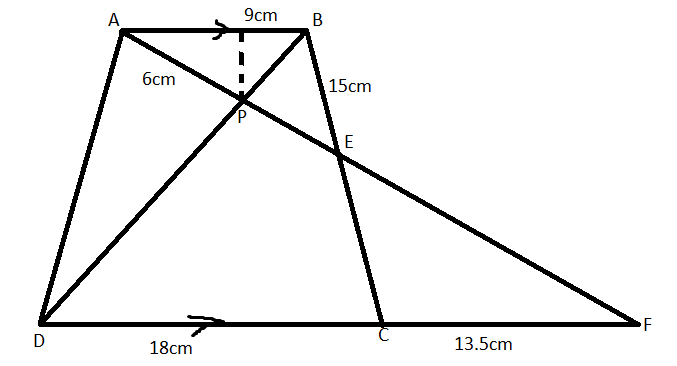
Now we have to prove that triangle APB and triangle BPE are similar. Now to prove that,
$\angle APD=\angle BPE$ (By the property of vertically opposite angle)
$\angle ADP=\angle EBP$ (By the property of alternate angles between two parallel line)
By using the angle-angle criteria, $\Delta APD\text{ and }\Delta BPE$ are similar triangles.
Since the above-mentioned triangles are similar, the ratio of the respective sides will be proportional. Equating this ratio, we get
$\begin{align}
  & \dfrac{PA}{PB}=\dfrac{PD}{PE}=\dfrac{AD}{BE} \\
 & \Rightarrow \dfrac{6}{BP}=\dfrac{PD}{PE}=\dfrac{AD}{15} \\
 & \Rightarrow \dfrac{6}{6}=\dfrac{AD}{15} \\
 & \therefore AD=15 \\
\end{align}$
Now, putting again in the above relation we obtain PE as:
$\begin{align}
  & \dfrac{PD}{PE}=\dfrac{AD}{BE} \\
 & PE=\dfrac{15\times 6}{18} \\
 & PE=4.8cm \\
\end{align}$
Therefore, the value of PE is 4.8cm.
Hence, option (b) is correct.

Note: The key concept involved in solving the problem is the knowledge of geometrical figures specifically trapezium and the concept of similar triangles. This knowledge is very useful in solving complex problems of geometry.