Question

In the following addition, A, B, C represent different digits. Find them and the sum

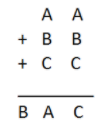
Answer 1

Hint:
Here we need to observe that by adding once place $A+B+C$ we are getting the first digit as $C$. How it can be possible. Unit place of $A+B$ has to be $0$. Then only on adding it with $C$ we’ll get $C$. Perform the similar analysis for tens place also to get the answer.

Complete step by step solution:
Here we observe that the last digit of $$A + B + C$$ is $$C$$, so that $$A + B = 10$$. Since $$C$$ is a digit, $$C \leqslant 9$$. Hence the carry from unit's place to ten's place is $$1$$.
Since we are adding only $$3$$ digits, the carry in ten's place of the sum cannot exceed $$2$$. Hence B cannot be more than $$2$$. Thus we observe that $$B = 1$$ or $$2$$. The addition of digits in ten's place gives (along with carry 1 from unit's place) $$A + B + C + 1 = 10 + C + 1$$and this must leave remainder $$A$$ when divided by $$10$$.
If $$B = 1$$, then $$A = 9$$ and hence $$C + 1 = 9$$ giving $$C = 8$$. We get $$99 + 11 + 88 = 198$$, which is a correct answer. If $$B = 2$$, you get $$A = 8$$ and $$C + 1 = 8$$ giving $$C = 7$$. But then $$88 + 22 + 77 = 187$$. This does not fit in a hundred's place in the sum is 1 but not 2.

The correct answer is $$99 + 11 + 88 = 198$$.

Note:
To solve such questions we need to understand the number system properly, especially the places and their value. There are a couple of variations of this question. Just to make the question easy, give a known number instead of giving all knowns.