Question

In the figure, write all pairs of adjacent angles and all the linear pairs.

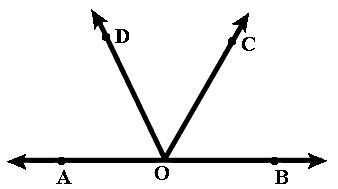
Answer 1

Hint: For solving this question, first we will see the definition of the adjacent angles, and linear pairs. After that, we will use these definitions to write the adjacent pair of angles present in the given figure and further we will use the definition to write the linear pairs present in the given figure easily.

Complete step-by-step answer:
Given:
We have to write all the pairs of adjacent angles and all the linear pairs in the following figure:

Now, before we proceed we should talk about the adjacent angles and what do we mean by linear pairs. So, first, we will go through their basic definitions and then we will give the answers to this problem.

Adjacent Angles:
Now, as we know that the measure of rotation of a ray, when it is rotated about its endpoint is known as the angle formed by the ray between its initial and final position. Moreover, the two angles are said to be adjacent angles when they share the common vertex and side. The endpoints of the ray forming the side of an angle is called the vertex of an angle. For more clarity, look at the figure given below:

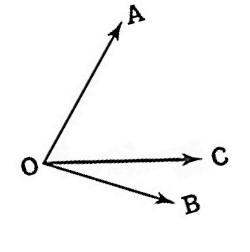
In the above figure, $\angle AOC$ and $\angle COB$ have a common vertex, a common arm and the uncommon arm lies on either side of the common arm. Such angles are known as adjacent angles.

Linear Pairs:
Now, as we know the meaning of adjacent angles, we can easily understand the concept of linear pairs. A pair of adjacent angles whose measures add up to form a straight angle is known as a linear pair. The angles in a linear pair are supplementary or in other words, if we take the uncommon arms of the pair of angles then we should get a perfect straight line. For more clarity, look at the following figure:

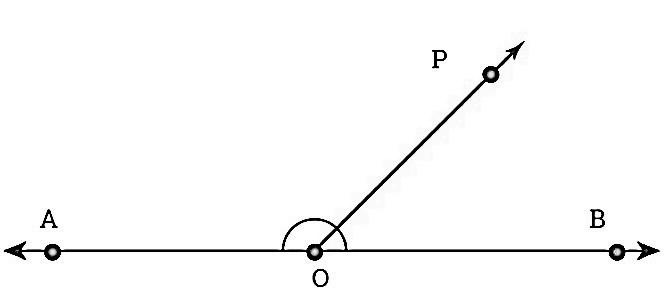
In the above figure, $\angle POB$ and $\angle POA$ are formed at point O. $\angle POB$ and $\angle POA$ are adjacent angles and they are supplementary i.e. $\angle POB+\angle POA={{180}^{\circ }}$ . $\angle POB$ and $\angle POA$ are adjacent to each other and when the sum of adjacent angles is ${{180}^{\circ }}$ then such angles form a linear pair of angles.
Now, we come back to our problem in which we have the following figure:

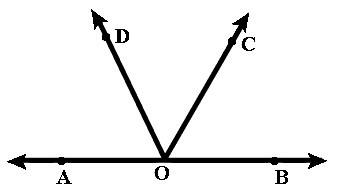
Now, according to the definition of the adjacent angles, we can say that a pair of angles, having a common vertex, a common arm and the uncommon arm lie on either side of the common arm will be considered as adjacent angles.
Now, by going through the given figure pairs of adjacent angles are given below:
\[\begin{align}
  & \angle AOD\And \angle DOC\text{ }\left( \text{common arm is OD and vertex is O} \right) \\
 & \angle AOD\And \angle BOD\text{ }\left( \text{common arm is OD and vertex is O} \right) \\
 & \angle BOC\And \angle DOC\text{ }\left( \text{common arm is OC and vertex is O} \right) \\
 & \angle BOC\And \angle AOC\text{ }\left( \text{common arm is OC and vertex is O} \right) \\
 & \angle AOB\And \angle AOD\text{ }\left( \text{common arm is OA and vertex is O} \right) \\
 & \angle AOB\And \angle AOC\text{ }\left( \text{common arm is OA and vertex is O} \right) \\
 & \angle AOB\And \angle BOC\text{ }\left( \text{common arm is OB and vertex is O} \right) \\
 & \angle AOB\And \angle BOD\text{ }\left( \text{common arm is OB and vertex is O} \right) \\
\end{align}\]
Now, from the above 8 pairs of adjacent angles, we can clearly say that, we have following two pairs which are supplementary:
$\begin{align}
  & \angle AOD+\angle BOD={{180}^{\circ }} \\
 & \angle AOC+\angle BOC={{180}^{\circ }} \\
\end{align}$
Now, from the definition of the linear pairs, we know that a pair of adjacent angles whose measures add up to form a straight angle is known as a linear pair. Moreover, the angles in a linear pair are supplementary. So, we conclude that, $\angle AOD\And \angle BOD$, $\angle AOC\And \angle BOC$ will be linear pairs.

Note: Here, the student should know the definitions of adjacent angles and linear pairs. After that, while solving we should always solve such questions by a figure only and first try to gather the data from the given figure and then, proceed further. Moreover, while writing the pair of adjacent angles don’t forget to write the adjacent pair for the $\angle AOB$ as it is also an angle of ${{180}^{\circ }}$.