Question

In the figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the center of each circular flower bed is the point of intersection of O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower bed.

Answer 1

Hint: Total area of the figure given can be found by taking the area of lawn and the two flower beds, i.e. area of square and the area of 2 segments formed. Here the 2 flower beds are of the same area.

Complete step-by-step answer:

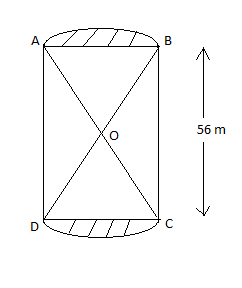
It is said that 2 circular flower beds are shown on 2 sides of the square lawn ABCD.
Thus to get the total area, it is the sum of the area of lawn and area of flower bed.
\[\therefore \]Total area = Area of lawn + Area of flower bed.
We can find the area of lawn ABCD, which is a square of side 56 m.
\[\therefore \]Area of lawn = Area of square \[={{\left( side \right)}^{2}}={{\left( 56 \right)}^{2}}=3136{{m}^{2}}.\]
\[\therefore \]Hence we got the area of the lawn \[=3136{{m}^{2}}.\]
Now we need to find the area of the flower beds AB and CD.
Area of flower bed AB = area of segment AB = Area of sector OAB – Area of \[\Delta OAB.\]

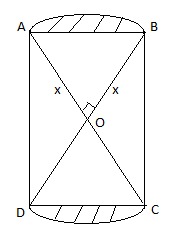
First let us find the length of OA and OB.
We know that the diagonals of a square bisect at right angles are equal.
\[\therefore \angle AOB={{90}^{\circ }}\] and OA = OB.
Let us put OA = OB = x.
Now, let us consider \[\Delta OAB.\]
By Pythagoras theorem,
\[\begin{align}
  & {{\left( hypotenuse \right)}^{2}}={{\left( height \right)}^{2}}+{{\left( base \right)}^{2}} \\
 & \therefore A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}} \\
\end{align}\]
We know that \[AB=56m\].
\[\begin{align}
  & \therefore {{\left( 56 \right)}^{2}}={{x}^{2}}+{{x}^{2}} \\
 & \therefore 2{{x}^{2}}={{\left( 56 \right)}^{2}} \\
 & \therefore {{x}^{2}}=56\times 28...........(1) \\
\end{align}\]
We know the area of sector \[=\dfrac{\theta }{360}\times \pi {{r}^{2}}.\]
\[\therefore \]Area of sector OAB, with \[\theta ={{90}^{\circ }}\] and r = x.
\[\therefore \]Area of sector OAB
\[\begin{align}
  & =\dfrac{90}{360}\times \pi {{x}^{2}} \\
 & =\dfrac{90}{360}\pi \left( 56\times 28 \right) \\
 & =\dfrac{1}{4}\times \dfrac{22}{7}\times 56\times 28 \\
 & =22\times 56 \\
 & =1232{{m}^{2.}} \\
\end{align}\] \[\begin{align}
  & \left[ \because {{x}^{2}}=56\times 28 \right] \\
 & \left[ Take:\pi ={}^{22}/{}_{7} \right] \\
\end{align}\]
Let us find the area of \[\Delta OAB.\]
The diagonals of a square divide the square into congruent triangles.
\[\therefore \Delta AOB\cong \Delta BOC\cong \Delta COD\cong \Delta AOD.\]
Thus all triangles are similar, i.e. congruent triangles have the same area.
\[\therefore ar\left( \Delta AOB \right)=ar\left( \Delta BOC \right)=ar\left( \Delta AOD \right).\]
which is equal to \[{{{}^{1}/{}_{4}}^{th}}\]of the area of square ABCD.
\[\begin{align}
  & \therefore 4ar\left( AOB \right)=ar\left( ABCD \right) \\
 & ar\left( AOB \right)=\dfrac{1}{4}ar\left( ABCD \right) \\
 & \therefore ar\left( AOB \right)=\dfrac{1}{4}\times 3136=784{{m}^{2}}. \\
\end{align}\]
\[\therefore \]Area of \[\Delta AOB=784{{m}^{2}}.\]
\[\therefore \]Area of flower bed = Area of sector AOB – Area of \[\Delta AOB=1232-784=448{{m}^{2}}.\]
Similarly by symmetry we can say that the area of flower bed CD is the same as area of flower bed AB \[=448{{m}^{2}}\].
\[\therefore \]Area of lawn + Area of flower bed
\[=3136+(448+448)=4032{{m}^{2}}\].
Thus we got the total area of the lawn and the flower beds as \[4032{{m}^{2}}\].

Note: We have used properties of squares to find the area of the triangles that are formed in the square, which will be of the same area and divide the square into 4 equal areas. Remember the formula for finding the area of a sector and prove that the angle formed between \[\angle AOB={{90}^{\circ }}\], so as to find the area of the sector.