Question

In the figure, the side QR of \[\Delta PQR\] is produced to a point S. If the bisectors of \[\angle PQR\] and \[\angle PRS\] meet at a point T, then prove that \[\angle QTR=\dfrac{1}{2}\angle QPR\].

Answer 1

Hint: In the \[\Delta PQR\], we have \[\angle PRS\] as an exterior angle. We know that the exterior angle is equal to the summation of the interior two angles. That is, \[\angle PQR+\angle QPR=\angle PRS\]. In the \[\Delta TQR\], we have \[\angle TRS\] as an exterior angle. We know that the exterior angle is equal to the summation of the interior two angles. That is, \[\angle TQR+\angle QTR=\angle TRS\]. We also have, \[\angle PQT=\angle TQR\] and \[\angle PRT=\angle TRS\] because QT and RT is the angle bisector of \[\angle PQR\] and \[\angle PRS\] respectively.

Complete step-by-step solution -

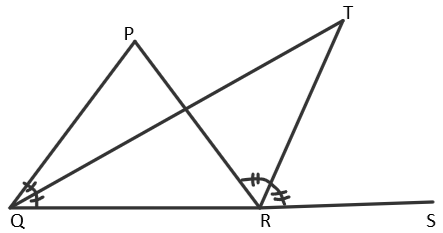
According to the figure given, we can see that we have two triangles which are \[\Delta PQR\] and \[\Delta TQR\].
In the \[\Delta PQR\], we have QT as an angle bisector and we know that angle bisector bisects an angle into two equal angles. So, we can say that
\[\angle PQT=\angle TQR\] ……………..(1)
Also, \[\angle PRS\] is an exterior angle for the \[\Delta PQR\] .
We know that for a triangle, the exterior angle is equal to the summation of the interior two angles. That is, \[\angle PQR+\angle QPR=\angle PRS\] ……………….(2)
Also, \[\angle PQR=\angle PQT+\angle TQR\] ………………….(3)
Using equation (3), we can write equation (2) as
\[\angle PQR+\angle QPR=\angle PRS\]
\[\angle PQT+\angle TQR+\angle QPR=\angle PRS\]
From equation (1), we have \[\angle PQT=\angle TQR\]
\[\angle TQR+\angle TQR+\angle QPR=\angle PRS\]
\[2\angle TQR+\angle QPR=\angle PRS\] ………………….(4)
We have RT as an angle bisector and we know that angle bisector bisects an angle into two equal angles. So, we can say that
\[\angle PRT=\angle TRS\] ……………..(5)
Also, \[\angle PRS\] is an exterior angle for the \[\Delta TQR\] .
We know that for a triangle, the exterior angle is equal to the summation of the interior two angles. That is, \[\angle TQR+\angle QTR=\angle TRS\] ……………….(6)
Also, \[\angle PRS=\angle PRT+\angle TRS\] …………(7)
From equation (5), we can write equation (7) as,
\[\angle PRS=\angle PRT+\angle TRS\]
\[\angle PRS=2\angle TRS\]
\[\dfrac{\angle PRS}{2}=\angle TRS\] …………………(8)
Now, using equation (8), equation (6) can be written as
\[\begin{align}
  & \angle TQR+\angle QTR=\angle TRS \\
 & \angle TQR+\angle QTR=\dfrac{\angle PRS}{2} \\
\end{align}\]
\[2\angle TQR+2\angle QTR=\angle PRS\] ………………….(9)
We can say that equation (4) and equation (9) are equal.
On comparing equation (4) and equation (9), we get
\[2\angle TQR+\angle QPR=2\angle TQR+2\angle QTR\]
\[\angle QPR=2\angle QTR\]
\[\angle QTR=\dfrac{1}{2}\angle QPR\]
Hence, \[\angle QTR=\dfrac{1}{2}\angle QPR\] .
Proved.

Note: As in this question, we have to use angle notation multiple times. So, one can easily get confused and do a mistake here. If someone is getting confused then the best way to solve this problem is to assume some variable term like \[\theta ,\alpha ,\beta \] , and \[\gamma \] to \[\angle QTR\] , \[\angle PQT=\angle TQR\] , \[\angle PRT=\angle TRS\] , and \[\angle QPR\] respectively.
We have two equations to solve which are
\[2\alpha +\gamma =2\beta \] ………………….(1)
\[\alpha +\theta =\beta \] ……………….(2)
Multiply by 2 in equation (2), we get
\[2\alpha +2\theta =2\beta \] ……………..(3)
Now, from equation (1) and equation (3), we get
\[2\alpha +\gamma =2\alpha +2\theta \]
On solving we get, \[\theta =\dfrac{\gamma }{2}\] .
We had assumed \[\theta =\angle QTR\] and \[\gamma =\angle QPR\] .
Hence, \[\angle QTR=\dfrac{1}{2}\angle QPR\] .
Proved.