Question

In the figure, the diameter CD of a circle with center O is perpendicular to the chord AB. If AB = 12 cm and CE = 3 cm, the radius of the circle is:

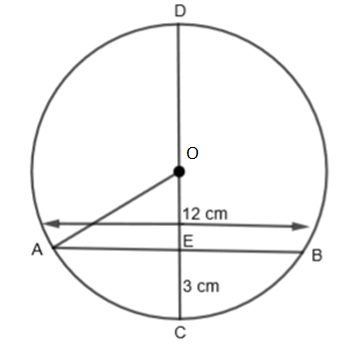
(a) 4.5 cm
(b) 9.5 cm
(c) 6.5 cm
(d) 7.5 cm

Answer 1

Hint: To solve this question, we will first prove that AE = EB. After proving this, we will derive the relations between OA, OE, and EC. After this, we will apply Pythagoras theorem in OAE and we will find the hypotenuse of the triangle which is equal to the radius of the given circle.

Complete step-by-step answer:
First, we will find the lengths AE and EB. For this, we will join the points O and B as shown:

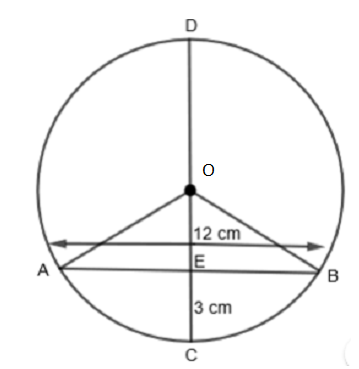
Here, we can say that OA = OB because they are radii of the circle. Also, \[\angle OEA=\angle OEB={{90}^{o}}\] because OC is the perpendicular to chord AB. Now, in the triangles OAE and OBE, we have,
OA = OB = radius (H)
\[\angle OEA=\angle OEB={{90}^{o}}\left( R \right)\]
OE = OE (Common Side) (S)
Thus the triangles OAE and OBE are congruent by RHS (Right – Angle – Hypotenuse – Side) rule. Thus, if two triangles are congruent, then we can say that AE = EB. It is also given that AB = 12 cm. Thus, we have:
AB = AE + EB
12 = AE + AE
2 AE = 12 cm
AE = 6 cm
Now, we know that OA and OC are both radii of the circle. Thus, we can say that,
OA = OC = r
OA = r…..(i)
OC = r
r = OE + EC
r = OE + 3
OE = r – 3……(ii)
Now, we will apply the Pythagoras theorem in the triangle OAE. According to Pythagoras theorem, we have,
\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\]
where H is the hypotenuse of the triangle. In our case, it is equal to radius OA. P is the perpendicular of the triangle. In this case, it is equal to the length OE. B is the base of the triangle. In our case, it is equal to length AE. Thus, we have:
\[{{\left( OA \right)}^{2}}={{\left( OE \right)}^{2}}+{{\left( AE \right)}^{2}}.....\left( iii \right)\]
Now, we will substitute the value of OA and OE from (ii) and (i) to (iii). After doing this, we will get:
\[{{\left( r \right)}^{2}}={{\left( r-3 \right)}^{2}}+{{\left( 6 \right)}^{2}}\]
\[{{r}^{2}}={{r}^{2}}-6r+9+36\]
\[6r=45\]
\[r=\dfrac{45}{6}\]
\[r=7.5cm\]
Hence, option (d) is the right answer.

Note: We can also prove the equality of AE and EB from the chords of the circle theorem. According to this theorem if a radius is perpendicular to the chord then that radius will be the perpendicular bisector of that chord. Thus, if the radius bisects the chord then AE = EB.